Non-Involute Gearing, Function and Manufacturing Compared to Established Gear Designs
Non-Involute Gearing, Function and Manufacturing Compared to Established Gear Designs
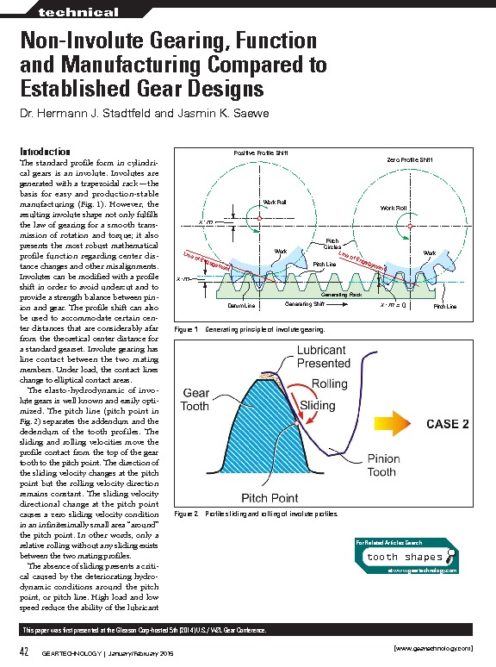
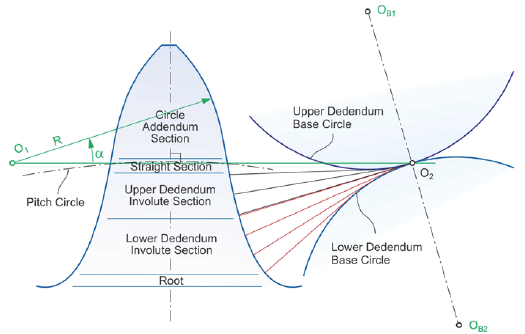
Introduction The standard profile form in cylindrical gears is an involute. Involutes are generated with a trapezoidal rack — the basis for easy and production-stable manufacturing (Fig. 1).
However, the resulting involute shape not only fulfills the law of gearing for a smooth transmission of rotation and torque; it also presents the most robust mathematical profile function regarding center distance changes and other misalignments. Involutes can be modified with a profile shift in order to avoid undercut and to provide a strength balance between pinion and gear. The profile shift can also be used to accommodate certain center distances that are considerably afar from the theoretical center distance for a standard gearset. Involute gearing has line contact between the two mating members. Under load, the contact lines change to elliptical contact areas.
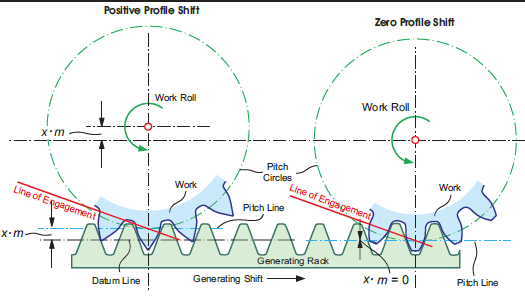
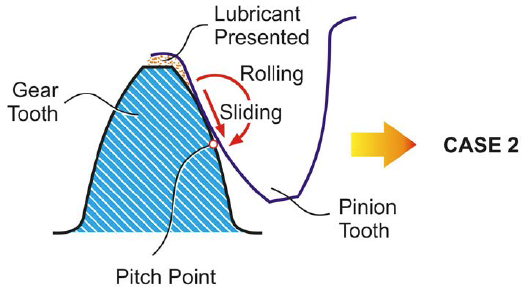
The elasto-hydrodynamic of involute gears is well known and easily optimized. The pitch line (pitch point in Fig. 2) separates the addendum and the dedendum of the tooth profiles. The sliding and rolling velocities move the profile contact from the top of the gear tooth to the pitch point.
The direction of the sliding velocity changes at the pitch point but the rolling velocity direction remains constant. The sliding velocity directional change at the pitch point causes a zero sliding velocity condition in an infinitesimally small area “around” the pitch point. In other words, only a relative rolling without any sliding exists between the two mating profiles.
The absence of sliding presents a critical caused by the deteriorating hydrodynamic conditions around the pitch point, or pitch line. High load and low speed reduce the ability of the lubricant to maintain a surface separating film. Good gear design and modern, high-performance oils can eliminate this pitch line phenomenon (Ref. 1).
Scientists and inventors frequently introduce new, non-involute gear profiles. The major target of those profile or tooth forms is the reduction of the relative curvature between the two contacting flanks in every roll position. Many of the proposed systems seem to have a close relationship to the cycloidal tooth profile as it is used in clocks and watches — or to the Wildhaber-Novikov design, first introduced by Ernest Wildhaber in 1910.
The main argument — often quoted as explanation — as to why those gear types have not been discussed and examined much earlier is the fact that current computation technology and mechanical machine tools of the past were incapable of utilizing both the complex tools as well as the complicated machine motions needed in order to create the non-involute profiles.
This paper discusses the proposed non-involute and involute-related profiles with their advantages and disadvantages. The criteria of the discussion are:
- Design calculation
- Analysis and optimization possibility
- Ease of tool manufacturing
- Accuracy of tool geometry
- Production-stable manufacturing
- Robust operating performance
After an analysis of alternative cylindrical gear tooth profiles, some new bevel and hypoid gear geometries that have been proposed during the past decade are discussed as possible replacements for the traditional face hobbing and face milling systems.
Involute-based cylindrical gears — as well as bevel and hypoid gears — went through a multiplication of their power density during the past 20 years. In order to create a fair discussion with objective comparisons, the last part of this paper is devoted to present the latest advancements of “traditional” involute gearing using the example of asymmetric cylindrical gear designs.
Cycloidal gears. Cycloidal gearing has been described as center distance maintaining. The S-shaped profile of the generating rack teeth will form S-shaped teeth and generate a force in the center distance direction in order to move the meshing gears to the correct center distance location (utilizing the axes play of the gears in watches).
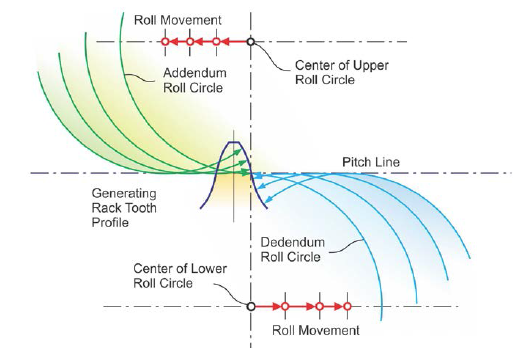
A development of a cycloidal generating rack tooth profile is shown in Figure 3. The reference line or pitch line separates the addendum and dedendum of the tooth. One roll circle, that is located above the pitch line, rolls to the left and generates — with one fixed point — the addendum of the right flank. A second roll circle rolls on the pitch line from below and generates the dedendum of the right flank (Fig. 3).
The two profile sections meet at the pitch line, where both cycloids have an infinitely high curvature. The cycloidal tooth profile is “S-shaped,” which achieves in the rolling interaction between mating flanks a large contact area on the flank surfaces. The convex addendum has constant rolling contact with the concave dedendum. Surface stress is greatly reduced compared to involute gears due to this arrangement, while the root bending stress can potentially be somewhat lower because of the concave dedendum profile, which blends without curvature reversal into the root fillet radius.
Cycloidal gear profiles can be generated with generating rack tooth profiles, like the one shown in Figure 3.Those profiles must be calculated and manufactured dependent upon the individual gear pair. Standard generating profiles — like the straight line in involute gearing — are not possible. Another possible process to manufacture cycloidal tooth profiles uses a pointed tool, which follows the cycloidal profile, guided either by cams or interpolating axes motions.
The tools to manufacture cycloidal gears are either special and, therefore, expensive, or the manufacturing process is very slow. The center distance-maintaining feature is only of interest if the axes’ position can float. In regular power transmissions, where the center distance is rigid, but might vary from the theoretical center distance, motion error and vibration are generated.
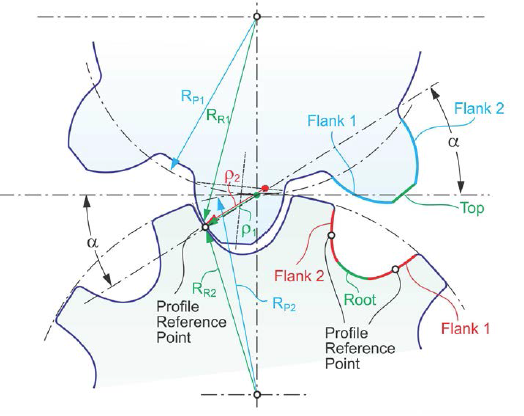
Wildhaber-Novikov gears. The Swissborn Ernest Wildhaber invented in 1926, shortly after his immigration to the United States and his employment as Gleason scientist, a helical gear profile which was cut with a circular arc profile rack cutter (Ref. 2). Thirty years later, Mikhail Novikov invented in Russia a similar system which featured tooth profiles that are circular in the transverse plane (Ref. 3). Because of the similarity of the two independent developments, cylindrical gears with circular tooth profile have been called Wildhaber-Novikov gears. Not only are the tooth profiles circular, but the slots of the gear have the appearance of half-circles and remind in its shape of a sprocket. Figure 4 reveals that the gear slots have profiles with two equal radii, connected with a smaller radius in the root, which blends with the flank radii. The pinion profile radii are smaller than the profile radii of the gear, and are connected at the top with a straight line.
In order to transmit a constant ratio, the contacting point between the two circular flank surfaces must be kept at the same profile location, which is preferably a point at mid-profile height with a desirable pressure angle. This point is called the “profile reference point” (Fig. 4).
The different radii of pinion and gear flanks (p1 and p2) have to be oriented normal to the profile reference point, but with a larger gear radius value and a smaller pinion radius value (Fig. 4, left). Keeping the contacting point in the same initial profile location (Fig. 4, left) during an incremental pinion (and gear) rotation can only be realized with the introduction of a helix angle; the helix angle must be defined such that for a certain pinion rotation the profile rotates back to the initial position. Subsequently, the gear profile also has to rotate back into the initial position by an angular amount equal to the angle of the pinion rotation, divided by the ratio between the two members.
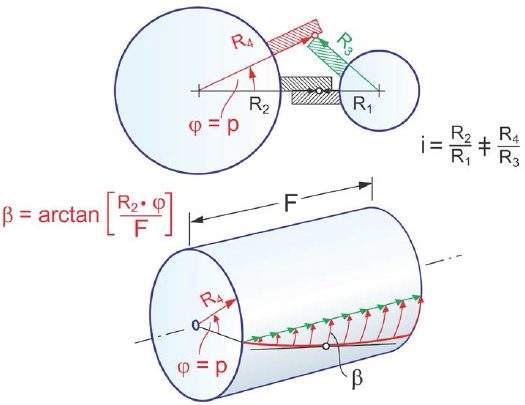
The method of corrective rotation of the tooth profile in order to transmit a constant ratio is visualized (Fig. 5).
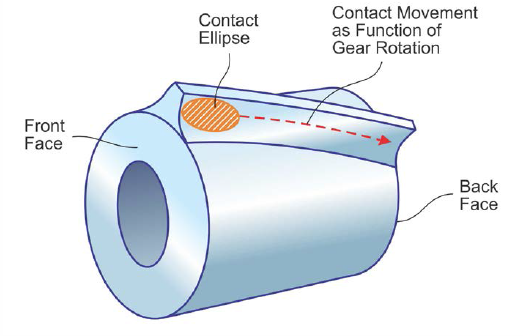
The first point of contact between the meshing teeth is shown in the upper graphic as the connecting point of R1 and R2. As the gears rotate to an advanced angular position, the radii R3 and R4 would transmit a different ratio because the vector length — as well as the normal vector direction — changed. The cylinder in the lower graphic demonstrates that if a flank line with a particular helix angle is used that rotates the contacting point for incremental rotations into the horizontal axis connecting plane, then contact movement (Fig. 6) can be expected. The ratio will remain constant in this case because the radii — and the normal vectors in the horizontal plane along the reference cylinders — remain constant.
A simple example: A pitch angle of 24° and a contact ratio of 1.0. If the pinion is rotated by 24° and the initial contact at the profile reference point is located at the front face of the teeth, then the back rotation of the profile has to occur as the contact moves along the face width to the back face of the teeth.
The helix angle at the reference radius is calculated: ßR = arctan (RR• P/F)
Example:
Given:

The example shows that a particular Wildhaber-Novikov gear design requires a particular helix angle that depends on the desired contact ratio and the face width. The explanation and the calculation also show that the transverse contact ratio of Wildhaber-Novikov gears is zero and the modified contact ratio is equal to the face contact ratio.
The advantages of circular tooth profile are the large contact area. Russian studies from the 1950s and 1960s report about three-to-five times the load-carrying capacity, without detrimental pitting or wear. The reports also state that the circular wedge geometry between the contacting circles that moves along the face width, pumps the lubricant into the contact area and generates oil film thicknesses up to 10 times that of involute gearing, which should also improve efficiency (Chironis). Disadvantages include the more complicated rack tool geometry, the high influence of the helix angle to the smoothness of transmission, as well as the sensitivity of center distance changes. The helix angle in Wildhaber-Novikov gears is not a design freedom like in involute gearing, but is exactly given for each particular design. The operating vibration and noise of Wildhaber-Novikov gears has been reported to be higher than that of comparable involute gears.
The original Wildhaber-Novikov tooth profiles are basically half-circles, which call for a certain pressure angle change between top and root. The end of the internal circle towards the top and the external circle towards the root are given by a pressure angle that drops below 5°. Because of this constraint, Wilhaber- Novikov teeth consist of less than a halfcircle, which results in tooth depths that are about 1.2 times the module, compared to 2.2 times the module for standard involute gears. The pressure angle change along the profile-per-unit-length in case of less than a half-circle is a multiple of the involute curvature change. This is an additional reason to the non-involute profile function for the high sensitivity to center distance changes of pure circular profile forms. The low-profile teeth show a very high stiffness, which often is falsely judged as an advantage and a contributor to high power density. More optimal is high stiffness at the root of the teeth and elasticity from mid-dedendum to the tip. The elasticity contributes to a reduced entrance impact during meshing at different loads and improves the load sharing between consecutive tooth pairs. In order to account for those facts, Wildhaber, as well as Novikov, mentioned in their teachings the possibility to extend their ideas to double-circular profiles that consist of a convex circle at the addendum and a concave circle at the dedendum (Fig. 7).
All variations of Wildhaber-Novikov gears can be manufactured by the hobbing and shaping processes. Depending upon whether the tooth normal profile or the tooth transverse profile should be of circular shape, the cutter rack profile must consist of modified curves (no circles) to accommodate for the generating motion between cutter and work. Also, the use of circular-shaped rack cutters is mentioned in the literature, which would of course generate complex non-circular profile curves.
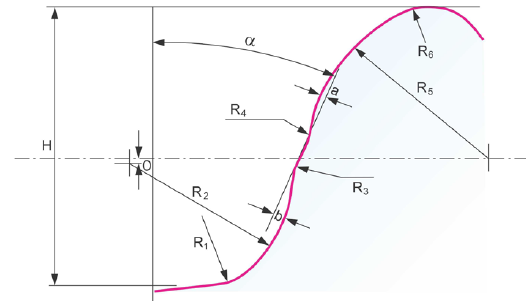
Profile development. Shigeyoshi Nagata, a professor at the University of Tokyo published a paper in 1981 where he discusses a proposed improvement of the extended Wildhaber-Novikov profile design (Ref. 4). Nagata bases the profile definitions not on the gear teeth, but on the rack cutter or reference profile. The basic construction of this profile is represented in Figure 8.
The new profile has a circular addendum and a dedendum that consists of two involutes that blend at mid-dedendum. The upper dedendum is developed with a cord — unrolled from the upper base circle — where the lower dedendum is developed with a cord that unrolls from the lower base circle. The addendum is circular (Fig. 8) and has a nominal pressure angle at mid-addendum.
Nagata shows in a theoretical evaluation a significant reduction in center distance sensitivity of the improved profile combination of circular and involute elements. In a following study, Nagata tested a variety of Wildhaber-Novikov-Nagata gears and published the results with recommendations for optimal parameters in 1985 (Nagata 85). The manufacture of Wildhaber-Novikov-Nagata gears is possible by hobbing and shaping. All common hard-finishing methods can also be applied if the tool profile is formed accordingly. Like in standard Wildhaber- Novikov gears, the helix angle is required and differs depending on the individual gear design.
Convoloid gearing. Bernard Berlinger and John Colbourne introduced in a paper, published in 2011, a tooth form called Convoloid (Ref. 5). The new tooth form appears optically very similar to the Wilhaber-Novikov-Nagata development (Fig. 9).
The addendum has a convex shape, while the dedendum is concave. The transition zone at the pitch point seems to be “S-shaped” rather than the straight section of Nagata’s development. The authors report that the tooth profiles are computer calculated as a point cloud for each application case individually.
One interesting conclusion of Berlinger’s and Colbourne’s findings is the fact that while involute gearing fit well with traditional, mechanical gear manufacturing machines, it is outdated for today’s engineering and manufacturing environment. Test rig investigations of Convoloid gears resulted in 20%-35% increased torque levels vs. involute gearing. The center distance insensitivity of involute gears seems not to be given, but the inventors state that the Convoloid gears can withstand the customary deflections given in modern gearboxes.
An interesting aspect of Convoloid gears is that the tooth contact can move from root to top while maintaining the correct ratio. This makes Convoloid gears independent from the helix angle and allows a choice of suitable helix angles, depending on gearbox application requirements. The Convoloid profile of Figure 9 refers to the final teeth, not to the rack profile. In order to establish the rack cutter profile, the kinematic rela-tionships, e.g., of a hobbing process, have to be employed to calculate a point-based cutting edge definition.
S-shaped tool profile for spiral bevel gear cutting. Stepan Lunin discussed a Wildhaber-Novikov-style profile for a bevel gear cutting tool in a paper published in 2001 (Ref. 6). The profile consists of radii and straight lines (Fig. 10).
The pitch line of spiral bevel gears is in all cases of non-miter gears located towards the pinion root (positive profile shift) which will create profile sliding at the location of the transition wave. Profile sliding during the generating process will eliminate or mutilate the transition wave, which makes the intention of the midsection of the proposed profile questionable.
The goal of using such a profile might be the reduction of unit surface pressure with an increase of power density. This could be accomplished with the extended Wildhaber-Novikov profile that would also eliminate the complicated tool midsection, which is not believed to serve any practical purpose. The paper doesn’t mention the relationship between profile and spiral angle. Because of the circular profile sections, it is assumed that the tool profile in Figure 10 requires — just as with the Wildhaber-Novikov gears — a particular spiral angle in order to maintain the correct transmission ratio during the meshing of the mating members. This will make the gearsets generated by the tool profile in Figure 10 sensitive to housing tolerances and deflections.
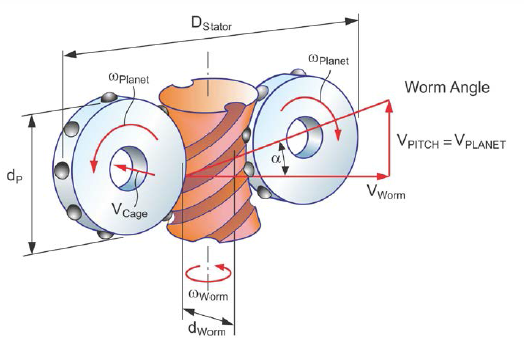
Toroidal drive. The inventor M.R. Kuehnle developed the idea of a compact and high-power- density, high-reduction planetary unit. The “heart” of the unit is a toroid which consists of a mounted upper and a lower “half-toroid” (Figure 11 shows the upper-half of the toroid ring gear).
The toroid has internal spherical threads that are the grooves for balls that connect the toroid with a sun gear via planets and planet carrier. The arrangement between center unit (sun gear worm), planets and planet carrier motion is shown in Figure 12.
The sun gear unit is a multi-start, spherical worm (similar to a throated worm) (Ref. 7).
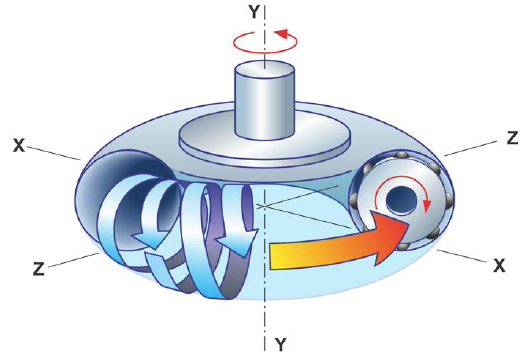
The toroid-shaped unit is normally used as the transmission housing. If the sun unit is used as an input shaft, then the planets will rotate along the grooves of the internal toroidal threads that initiate a slow cage rotation (cage as output shaft). The principle of planet and cage rotation is shown in Figure 13.
The inventive properties of the toroidal gearbox are high reduction with compact gearbox (high power density) and low wear.In order to streamline the design of the toroidal gearbox and verify the attributes of its functionality with scientific data, the inventor consulted the Institute of Machine Elements of the Technical University of Aachen. The scientists and engineers at the institute brought all components to a high level of mechanical design and manufacturability.
Kuehnle stated his toroidal transmission will out-perform worm gear, planetary and cycloidal transmissions for medium to high ratios. Center worm and planet units seem straightforward in manufacturing and assembly. However, the spiral grooves in the split, internal toroidal gear components are difficult to manufacture and will, post-assembly, present a disturbance in the smooth rolling of the balls at the fitting seam.
Globoidal gearing. Yakov Fleytman in 1999 invented a tooth form that mostly applies to hypoid gears. Fleytman claims the strength of his new hypoid gear design is three times that of traditional hypoid gears (Ref. 8). It seems that the creation of the gear tooth was done by using simple straight or twisted surfaces. The pinion flank surfaces might have been generated with simulation software, similar to Vericut. The gear can be defined as a tool and the axis positions of pinion and gear in a given hypoid gear box can be used as tool and work position in order to simulate the generating process of the pinion flank surfaces. Fleytman uses the kinematic coupling condition to generate the pinion teeth where the gear is used as a generating element. Flank profile and tooth lead form seem different to common bevel and hypoid gears because no customary profile requirements are mentioned and the equivalent pitch elements are not related to the transmission ratio (Fig. 14).
Globoidal gears cannot be manufactured using traditional manufacturing methods. Prototypes have been manufactured with 5-axis machines, but no reports of evaluation results have become public.
Cosine gears. HPG in the Netherlands, a company that developed 5-axis machining technologies for the soft and hard manufacture of bevel gears, introduced in 2007 a bevel gear with a sinusoidally formed flank line with the claim of 40% increased load-carrying capacity (Ref. 9). The teeth of that system have some similarity with the “herringbone” teeth in cylindrical gearing. The observer of the photographs in Figure 15 notices large variations of the tooth thickness and a curvature inflection point at each side of the center. It appears that the reason why the inventor anticipates a higher strength could be given by the curved profile in the center of the face width. The reversal with a lowering of the spiral angle towards the ends of the teeth seems unjustified and results basically in teeth with no spiral angle — which gives them similar properties to ZEROL bevel gears. Real herringbone gears are two connected helical gears with opposite helix angle directions. The advantage is a complete cancellation of all axial forces, combined with a very smooth mesh characteristic in their operation. The two opposing sections of herringbone gears are separated by a groove in order to eliminate the singularity at the point of helix angle change. This common herringbone gear design takes advantage of the smooth meshing and the high strength of helical gears without the disadvantage of rolling disturbance in the transition area between right- and left-hand sections.
It appears that the developers of the gear in Figure 15 supposed that the separation groove of herringbone gears is strictly the result of a manufacturing limitation of the traditional manufacturing methods and believed that the curved flank line at the center of the face width would increase the strength. The additional reversal of the flank line curvature towards the end of the teeth is probably also only done because it wouldn’t be possible in traditional manufacturing.
Meshing conditions of bevel gears without a spiral angle are best with straight bevel gears and deteriorate with ZEROL bevel gears. The smooth screwing into mesh like in spiral bevel gearing is not possible with the cosine teeth in Figure 15.
The face contact ratio is slightly above zero and will not contribute to improved strength. The cosine-shaped tooth form prevents elastic deformation under load, which in spiral bevel gears is used to achieve a smooth meshing and to increase the load-sharing between consecutive tooth pairs. Hartmuth Müller published theoretical investigation results of bevel gears with sinusoidally shaped flank lines and concluded that their rolling performance — as well as their strength properties — is far below any average spiral bevel gear set (Ref. 10).
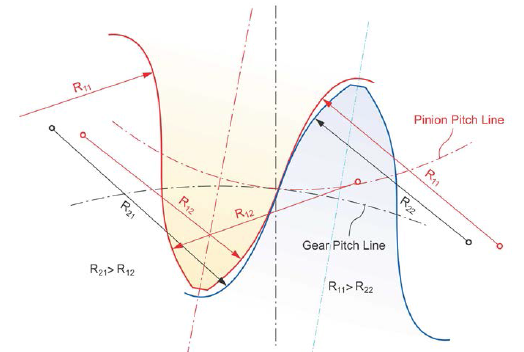
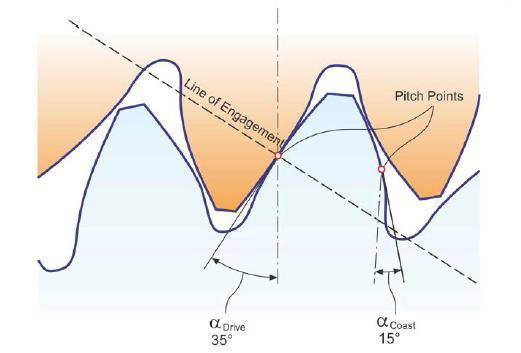
Asymmetric tooth gears. The two flank profiles of involute gearing are generally developed from a common base circle. In this case both flank profiles have the same pressure angle and are mirror images from each other. With the development of hypoid gears, Ernest Wildhaber in 1930 developed the asymmetric tooth profile (Ref. 11). Wildhaber’s development eliminated the conflict that the path of engagement of the drive-side flanks and the coast-side flanks was not equal if hypoid gears were manufactured with equal pressure angles.
Today, asymmetric spur gear profiles that have been proposed for more than 20 years are discussed and applied to practical applications. The goal is not to extend the angle of engagement, as it was for Wildhaber, on the drive-side of hypoid gears. Extending the active line of engagement would require a reduction of the pressure angle. Alfonso Fuentes et al. (Ref. 11) proved in an analytic comparison that especially flank surface stress is reduced on the driving side by increasing the pressure angle. A tooth mesh with asymmetric pressure angles is shown in Figure 16.
Alexander Kapelevich promoted asymmetric cylindrical gears for many years (Ref. 12) and wrote calculation software that allows design calculations for optimized geometries.
The problem is not only the manufacturing of asymmetric spur gears. It seems to be the fact that additional optimizations — like circular top relief — have to be applied in order to make the improvement visible. Fuentes developed first an optimal top relief for a baseline design and then converted the gearset to asymmetric profile. However, he created comparable gearsets with symmetric and asymmetric profile and was able to achieve contact stress reductions in the vicinity of 10%.
Several bevel gear manufacturers accepted the publications’ findings and research in asymmetric spur gears and applied moderate amounts (up to 4°) of asymmetric pressure angles to their traditionally symmetric spiral bevel gears in order to improve the load-carrying capacity of mostly unidirectionalused angular transmissions. The positive experiences with spiral bevel gears allow the conclusion that, not only spur gears, but also helical gears would benefit from asymmetric profiles. Because of the individually ground cutting blade profiles, this technology seems to gain more acceptance in bevel gearing. For cylindrical gears the introduction of asymmetric profiles would require a departure from standard hobs and may require additional profile corrections in order to work out the full advantages of asymmetric gearing, which seems to be a large step and thus precludes ready acceptance in the industry.
Summary
The tooth shapes discussed here can be sorted into those with interesting physical properties and those without sufficiently proven functionality. It is quite true that validating a new system is difficult if the technical community rejects the idea based on solely subjective reasons. This would prevent any private or public research funding. However, many of the new tooth profile solutions discussed in this paper are based on brilliant ideas that failed to have a breakthrough for similar reasons, as why, for example, the Wankel engine never replaced the stroking piston engine.
Cycloidal gears have been used for watches and clocks. Even though they are center distance-sensitive, the watch designer allows rather large center tolerances in connection with axle bearing play. The “S-shaped” profiles of the mating cycloidal gears develop a self-centering force that forces the gears to roll with correct center distance. The advantage of this design was the manufacturing cost reduction due to large bearing position tolerances and large axle play. The large bearing play in turn would guarantee low friction in the sleeve bearings, which achieves one important objective of chronometers. Manufacturing of the cycloidal requires specially formed tool profiles, or pointed tools, that move along a cycloidal path. The advantages cycloidal gears have in watches cannot be duplicated in industrial power transmissions.
Wildhaber-Novikov gears have proven their increased load-carrying capacity, yet show significant center distance sensitivity, are difficult to manufacture, require non-standard tools and depend on a specific, pre-determined helix angle in order to transmit a constant ratio. Changes in center distance and axes inclinations due to tolerances and deflections will introduce significant motion errors and transmission vibrations, which would increase the cost for shafts, bearings and/or housing in order to reduce tolerances and deflections. Even then, the robustness and “mechanical intelligence” of involute gearing that provides them with smooth rolling through many million cycles could not be achieved. The extended version of the Wildhaber-Novikov profile has an “S-shape” — just like the Cycloidal profile that adds the self-centering ability to the properties of the “half-round” profile of Figure 4.
The Nagata development is very similar to the extended Wildhaber-Novikov, but requires rather more complicated tool geometry. The “S-shaped” profile makes it an additional version of the Cycloidal gear type with similar physical properties. Center distance sensibility and difficult manufacturability also prevented the introduction of this gear type in power transmissions.
Convoloid gears, with their dedendum transition point, which is a “flat spot†in a finite profile section, cannot accept significant center distance changes. The flat section of the two mating profiles must be located precisely during the rolling process to separate addendum and dedendum rolling. The separation may interrupt the hydrodynamic lubrication, and misalignments may cause rolling of the transition flat into addendum or dedendum, which will create roll interference. The transition flat prevents or complicates the profile generation with a reference profile on a tool like a hob. Convoloid profiles seem to present the disadvantages of cycloidal profiles, with increased vulnerability around the pitch line.
The "S-shaped" bevel gear profile is very similar to the Convoloid profile. However, where the Convoloid profile is the result of an analytical mesh and contact area optimization, the singularity of the “S-shapedâ€Â bevel gear profile in mid-profile will not permit relative profile sliding in this section; this makes this proposed profile unusable in practical applications.
Globoidal gears use the kinematic coupling conditions of formate gears. The profile of the gear member is basically chosen to be straight and the pinion member is generated with respect to the desired ratio, shaft angle and center distance. The principle of interacting pitch elements is not applied, which leads to high relative sliding and can cause partial mutilation to the flank surface.
Cosine gears have been discussed to also elaborate on flank line ideas which do not conform to the common mathematical flank line functions. Cosine gears might have the ability to hold higher torques in a non-rotating, static condition. The attempt to design a gearset with performance advantages resulted in this case in load-carrying capacity similar to straight bevel gears, and a rolling performance that cannot compare to standard spiral bevel gears.
Asymmetric gears build upon the strength of involute gearing, with the acknowledgement that in case of a preferred driving direction, the properties of the driving flanks can be improved by taking away from the non-driving, or coasting, flanks. The practical results of transmissions with asymmetric gears show a significant increase of power density due to an improvement of root bending strength and higher surface durability. Investigations showed that the full advantage of asymmetric gearing vs. gears with symmetric involutes can only be realized if sensible tip relief modifications are applied. This in turn creates a problem for many manufacturers — even those that mass-produce, say, automotive transmissions. The wealth of experience that has been compiled over decades that found its way into the international standards, as well as the material application tables, has no or only limited use for the dimensioning and design of asymmetric gears. Also, the cutting tools are now not standard tools anymore. Different pressure angle offsets for different applications and gear design parameters in connection with circular tip relieves of different amounts will not only make existing tooling obsolete but also eliminate today's standards in hobs and even shaper cutters which will result in increased cutting tool cost and contribute to longer tooling lead times. The fact that asymmetric gears have not had a breakthrough yet is the result of those obstacles. However, the symmetry offset, as well as tip reliefs or other corrections, could be standardized, depending on module and application, which would remove the major obstacle for the broad application of asymmetric involute gears.
Conclusions
The motivation to change from involute profiles and proven straight or curved flank lines to alternative shapes is fueled by the logic that, in today’s time and age, more than just incremental improvements should be possible, applying new theories and sophisticated computation technology. Those dramatic improve-ments would consequently lead to geometries that would appear exotic if observed with the traditional viewpoint. The objective of this paper was to observe the published alternative tooth forms with an open mind in order to find objective answers to the question of why the interesting and sophisticated tooth form proposals haven’t had a breakthrough in the gear manufacturing industry. In angular gear drives, the absence of tight standards, as they exist for cylindrical gears, led to many gear types with different profile and lead functions. The fact that bevel gear cutting tools have never been standardized opened the door for this variety of different processes and tooth forms. The downside is that bevel gear design and manufacturing is perceived as complicated, not straightforward — and expensive. The standards in cylindrical gears, which are based on standard reference profiles and involutes, make design and manufacturing transparent and keep the cost of cylindrical gear manufacturing relatively low.
The center distance insensitivity of involute gears also applies in the relationship between generating rack and work gear and therefore makes hobbing a very robust process. The fact that every point along the involute has a normal direction that is tangent to the base circle gives the involute its robustness during manufacturing and in operation (Fig. 17) (Ref. 13). All of the discussed non-involute gears are sensitive to center distance changes and require individual tool designs. Standardization is not possible or difficult, which presents an additional risk in design and manufacturing. If higher load-carrying capacity, lower noise and increased efficiency are goals of new gear geometries, then the absence of standards and higher design and manufacturing cost might be acceptable in some cases. However, the physical properties of involute gearing are superior to most of the discussed non-involute gears. The potential of asymmetric, involute tooth profile will allow significantly improved cylindrical gears by maintaining the advantages of involutes. A broader interest on asymmetric gears could initiate the development of new standards and would — over time — allow the gear community to gain sufficient experience in this advanced system.
Nevertheless, it seems fair to say: “The involute is here to stay.”

References
- Stadtfeld, H.J. Gleason Bevel Gear Technology —The Science of Gear Engineering and modern Manufacturing Methods for Angular Transmissions, Gleason Publication, ISBN 978-0- 615-96492-8, 2014.
- Wildhaber, E. “Gears with Circular Tooth Profile Similar to the Novikov System,” VDI Berichte, No. 47, 1961, Germany.
- Novikov, M.L. USSR Patent No. 109,750, 1956.
- Nagata, S. And Y Ariga. “Development of a New Wildhaber-Novikov Gear with a Basic Rack of Combined Circular and Involute Profile, ” International Symposium on Gearing & Power Transmission, Tokyo, 1981.
- Berlinger, B.E. and J.R. Colbourne. “Convoloid Gearing Technology,” Gear Solutions, Media Solutions, INC Publishing, February 2012.
- Lunin, S. “New Methods of Gear Geometry Calculation,” the JSME International Conference on Motion and Power Transmission, The Japan Society of Mechanical Engineering, Fukuoka, Nov. 15, 2001.
- Troeder, C. “Toroid-Getriebe Forschungsvereinigung Antriebstechnik,” FVA Information Congress, Karlsruhe, November 1975.
- Fleytman, Y. Worm Gear Transmission United States Patent No. 6,148,683, November 2000.
- Schlossig H.P. Auf einfachem Weg zu guten Zähnen Werkstatt und Betrieb, Carl Hanser Publishing, Munich, April 2007.
- Mueller H. “Function Oriented 5-Axes Machining of Bevel Gears” Seminar “Innovations in Bevel Gear Technology,” WZL, Technical University Aachen, March 2012.
- Fuentes, A. “On the Behaviour of Asymmetric Cylindrical Gears in Gear Transmissions” SAEChina and FISITA (eds., Proceedings of the FISTA 2012 World Automotive Congress, DOI: 10.1007/978-3-642-33744-4_13, Springer- Verlag, Berlin, Heidelberg 2013.
- Kappelevich, A. “Asymmetric Gears:Parameter Selection Approach,” Gear Technology, June/July 2012, Pages 48-51, Randall Publishing Inc., Elk Grove Village, Illinois.
- Stadtfeld, H.J. “Operating Pressure Angle,” Gear Technology, May 2013, Pages 57–58, Randall Publishing Inc., Elk Grove Village, Illinois.