Management Summary
Currently, legislation is in place in the United Kingdom to encourage a reduction in energy usage. As such, there is an increased demand for machinery with higher efficiencies, not only to reduce the operational costs of the machinery,but also to cut capital expenditure. The power losses associated with the gear mesh can be divided into speed-and load-dependent losses. This article reviews some of the mathematical models proposed for the individual components associated with these losses, such as windage, churning, sliding and rolling friction losses. A mathematical model is proposed to predict the power losses on helical gears highlighting the major contributor to losses in the gear mesh. Furthermore, the mathematical model is validated with a case study.

Introduction
To meet the increased demand for machinery with higher efficiencies, suppliers must design equipment that reduces the operational costs of the machinery and cuts capital expenditure.

In the past, gears have been considered as highly efficient in transmitting loads, but the requirements from the customer to achieve a minimum efficiency target and penalties for noncompliance are becoming more and more stringent. A reduction in the power loss of a gearbox will cut the running costs of the equipment as it becomes more efficient and also uses less lubricant to cool the gear teeth. This in turn will reduce the size of the auxiliary equipment, such as the lubrication pump, and will also lead to a reduction in the heat exchanger capacity. All this will contribute to an overall smaller footprint of the equipment, which saves space that can be at a premium in some applications.

The power losses consist of speed-and load-dependent losses. Speed-dependent losses can be divided into windage losses, churning losses, bearing churning losses and seal losses. The load-dependent losses are made up of sliding friction loss, rolling friction loss and bearing loss.

Speed-Dependent Losses
Windage losses. As gears rotate, lubricant is flung off the gear teeth in small oil droplets due to the centrifugal force acting on the lubricant. These lubricant droplets create a fine mist of oil that is suspended inside the gear housing/case. The effect of this oil mist is an increase in "windage frictional resistance" on the gears and hence an increase in the power consumption. In addition, the expulsion of the oily atmosphere from the tooth spaces as the gear teeth come into engagement creates turbulence within the gearbox and increases the power consumption. The combination of these factors, as well as the losses at the side faces of the gears, contribute to the total windage losses. Factors that influence the magnitude of the windage loss include the rotational speed of the gear because power losses rise with an increase in peripheral velocity. Other factors are the tooth module, the amount of oil mist present inside the casing and the diameter of the gears.

A mathematical model to predict windage loss was proposed by Anderson et al. (Refs .1-2). However, Anderson’s windage loss equation accounted for neither the tooth module nor the helix angle. Townsend detailed a windage loss equation which included an oil mixture function φ and a gearbox space function λ and is presented here as Equation 1 (Ref. 3). The oil mixture function φ indicates the state/type of atmosphere inside the gear unit with φ = 1 indicating an oil-free atmosphere. The gearbox space function λ is set at 1 for free space and reduces to a value of 0.5 for a closely fitting enclosure, i.e. the fitting of baffles or shrouds around the gear.

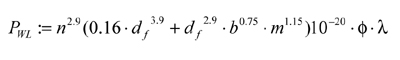(1)

Oil Churning Loss. Townsend defined churning losses as the action of the gears moving the lubricant inside the gear case and referred in particular to the losses due to entrapment of the lubricant in the gear mesh, which is more applicable to spur gears than to helical gears (Ref. 3).

Factors influencing the oil churning loss are the viscosity of the oil, as this resists the motion of the gears; peripheral velocity; operating temperature; the tooth module; the helix angle; and the submerged depth of the gears. All rotating components that are in direct contact with the lubricant, i.e. dipped into the oil, contribute to the churning losses, and the deeper the components are submerged, the higher the losses. With larger helix angles, the power losses are lower as the gear teeth slice through the lubricant rather than displacing the lubricant along the whole gear face width. Other expressions for determining churning losses have been proposed (Ref. 4). The British Standard BS ISO/TR 14179 Part 1 details churning loss equations which had been modified for the effect of lubricant viscosity, element diameter, the gear dip factor and the arrangement constant (Ref. 5). These churning loss expressions were split into three different sections, which are detailed in Equations 2-4.

Churning Loss for Smooth Outside Diameters (i.e. shafts):
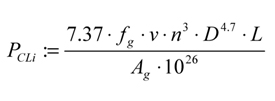(2)

Churning Loss for Smooth Sides of Discs (i.e. gear side faces, both faces):
(3)

Churning Loss for Tooth Surfaces:
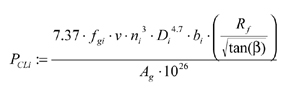(4)

Load-Dependent Losses
Sliding friction loss. Principally, the instantaneous sliding friction loss is a function of the instantaneous sliding velocity and the friction force, which itself is a function of the instantaneous normal tooth load and the instantaneous coefficient of friction. The magnitude of sliding velocity depends on the position of contact along the contact path with a peak velocity at the start of the approach. The velocity reduces to 0 at the pitch point of the two mating gears and rises again to a peak value at the end of the recess. The effect of the sliding friction loss is an increase in power consumption, where the magnitude depends on the point of contact. It is influenced by the angular velocity of the gears, the ratio of the rolling velocities, the point of contact, the contact ratio and the lubricant properties.

Anderson et al. analyzed the sliding friction losses along the path of contact and postulated expressions for the instantaneous sliding velocity and instantaneous friction force, where the friction force was a function of the instantaneous coefficient of friction and gear load. The sliding friction loss is dependent on the position of contact during the engagement cycle (Refs. 1-2). While the model proposed was specific for spur gears, the authors have modified the expression for the instantaneous coefficient of friction to include helical gearing. This was accomplished by modifying the expression for instantaneous coefficient of friction to take into account the helical gear contact length.

The instantaneous sliding power loss is given as:
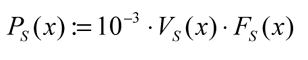(5)

where
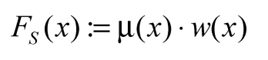(6)

The postulated expression proposed by Anderson et al. for the instantaneous coefficient of friction for spur gears is detailed in Equation 7 and was employed by the authors for this investigation (Refs. 1-2). The coefficient of friction is given as:

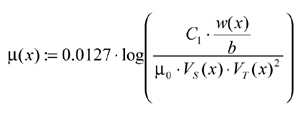(7)

The contact length for helical gears, Lc, has been detailed and was substituted by the authors into Equation 7 (Ref. 7). Therefore, the modified equation for the coefficient of friction for helical gears is given as:

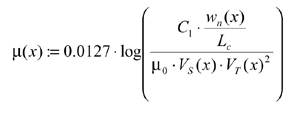(8)

The coefficient of friction used in this analysis is independent of the gear surface temperature, which--strictly speaking--is inaccurate. The expression in Equation 8 was substituted into Equation 6 to obtain the sliding power losses.

Rolling friction loss. The rolling friction loss is dependent on the instantaneous rolling velocity and the instantaneous lubricant film thickness. As the gear teeth come into mesh, an elastohydrodynamic lubricant film is developed between the teeth in contact. The action of the gear teeth during the engagement draws the lubricant into the contact zone. The parameters that influence the rolling friction loss are the lubricant film thickness, the angular velocity of the gears, the working pressure angle and the point of contact along its contact path. The lubricant properties influence the buildup of the lubricant film, its shear values and its thermal behavior. In addition, the gear material and the normal tooth load also influence the film thickness. In References 1-2, Anderson et al. postulated the instantaneous rolling friction force as:

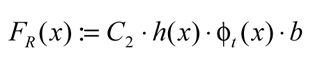(9)

where the rolling power loss is given as:
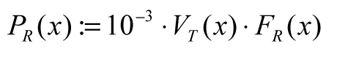(10)

This expression for instantaneous rolling force includes a thermal reduction factor that accounts for the decrease in oil film thickness as the pitch-line velocity increases (Ref. 6). A relationship between thermal loading factor and reduction factor was presented by Anderson et al. and employed by the authors of this investigation (Ref. 1). The paper by Anderson et al. implied that prior to computing the thermal reduction factor, the thermal loading factor must be determined. To account for helical gears, the expression of Equation 12 was modified by the authors, as the contact line length in helical gears is not synonymous with the face width. The modified instantaneous rolling force is given as:

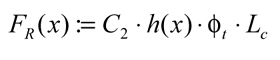(11)

where Lc, has been defined as the contact length for helical gears. The expression was substituted into Equation 10 to obtain the sliding power losses.

Mathematical Model
The mathematical model employed for this investigation consisted of the following expressions: 1. The windage loss equation as employed by Townsend (Ref. 3). 2. Churning loss expressions as detailed in BS ISO/TR 14179, Part 1 (Ref. 5). 3. The rolling and sliding friction losses as postulated by Anderson et al. (Ref. 1).

Model Validation
The gearbox used to validate the model was a single-stage, double-helical, speed-increasing gear unit with oil film bearings of the circular type. The inlet oil temperature was 49°C, and the maximum bearing temperature did not exceed 87°C. The input shaft and the output shaft end were sealed by means of a shaft-mounted oil flinger and non-contacting baffle rings in the housing. A lubrication pump was driven via a set of reduction gears from the input shaft. The pump supplied the lubricant for the gear sprayers and the force-fed bearing. The gear unit was tested in a back-to-back arrangement (see Fig. 1). A torque loader was fitted between the output shaft coupling end of the slave unit and the output shaft tail end of the test unit. The torque loader used for the experiment employed a pressurized oil system. The oil was supplied via a rotary union (see Fig. 1). The torque loader consists of an inner rotor and outer rotor, which are supported in bearings. Oil is fed into the space between the two rotors, creating a torsional load in the test rig. The bearing losses in the torque loader were calculated separately beforehand and subtracted from the motor input power prior to calculating the gearbox efficiency.

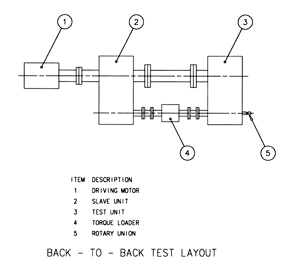
Figure 1--Schematic of the back-to-back arrangement for the high-speed gear unit.

The load conditions for the experiment included 25%, 50%, 75%,and 100% of full load (8.95 MWatts), at 100% input speed (1,460 rpm). Experimental torque readings were taken with a telemetric system from the low speed shaft via strain gauges. Appendix A details some gear data. It must be noted that the rig was run at full load and maximum speed (1,460 rpm) for a period of four hours. Prior to undertaking this test,the gear unit was visually inspected to ensure gear contact markings were satisfactory full face and full depth.

The mathematical model for the helical gears in this instance was accomplished by doubling the face width. The oil mix function was assumed to be φ = 3 and the gearbox space function was taken as λ = 1 as the gear case walls were sufficiently far away from the gears to be considered as free space. No oil churning took place, as this was a spray-lubricated arrangement. The experimental results provided the efficiency for the complete gear unit; therefore, the bearing losses, seal losses and absorbed power for the lubrication pump had to be calculated from manufacturer’s information (see Appendix B). The power loss calculations for the bearings assumed the maximum clearance condition. As non-contacting seals were employed, no power losses from the seals were assumed.

As the lubrication pump reduction gears were not separately sprayed, the oil mist present inside the gear case was assumed sufficient to provide lubrication. Again the same oil mix function and gearbox space function were assumed. The total predicted power losses were the sum of the losses from the lubrication pump and the gearbox. Results are detailed in Table 1. A comparison between predicted and experimentally determined power losses is shown in Figure 2. The model predicts a steady decline in power loss corresponding to a reduction in load.

Table 1--Experimental and Theoretical Results of Experiment I.
Power input (kW)	8,952	6,714	4,476	2,238
%load	100%	75%	50%	25%
Experimental total loss (kW)	125.33	116.82	112.35	106.75
Experimental total loss (kW)for gear and windage only	55.08	50.15	50.16	49.42
Predicted total loss (kW)	57.41	53.3	49.86	47.42
Breakdown of Losses
Sliding friction loss (kW)	10.88	6.672	3.05	0.34
Rolling friction loss (kW)	5.71	5.821	5.98	6.27
Churning loss (kW)	0	0	0	0
Windage loss (kW)	40.82	40.82	40.82	40.82

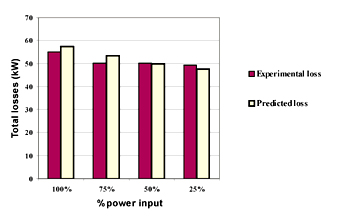
Figure 2--Comparison between experimental gear and windage losses and predicted power losses.

It was observed that by increasing the power input at a fixed rotational speed, the windage losses remained the same and the rolling friction power losses decreased while the sliding loss increased.

Discussion and Conclusion
The mathematical model detailed in this paper has shown to be valid, providing an indication of the contribution of each element within a gearbox with helical gearing to the total power loss. The predictions and the experimental results show a good correlation, although the experimental results do not provide a breakdown of the various power losses. In the breakdown of losses in Experiment I, it can clearly be seen that the sliding friction losses are heavily load dependent, increasing with load. However, the rolling friction losses decreased slightly with an increased load, and this is due to a decrease in oil film thickness. As the speed was constant during the experiment, windage losses remained constant throughout the tests.

This investigation did not review or include new mathematical models for load-dependent bearing losses and speed-dependent bearing churning and seal losses.

Acknowledgments
The authors wish to express their gratitude to David Brown, Textron Power Transmission for allowing the publication of this investigation, undertaken as a degree project for a master’s of science in Design of Rotating Machines, Cranfield University. This paper was presented at the ASME/AGMA 2003 International Power Transmission and Gearing Conference, held Sept. 3-5, 2003, in Chicago, IL, and was published in Proceedings of the 2003 ASME Design Engineering Technical Conferences & Computers and Information in Engineering Conference. It is republished here with permission from ASME.

References

1. Anderson, N.E., and S.H. Loewenthal. "Spur gear system efficiency at part and full load," Technical Report 79-46. NASA Technical Paper 1622, 1980.

2. Anderson, N.E., and S.H. Loewenthal. "Efficiency of nonstandard and high contact ratio involute spur gears," Journal of Mechanisms, Transmissions, and Automation in Design, Vol. 108, March 1986, pp. 119-126.

3. Townsend, D.P. "Lubrication and cooling for high speed gears," Original Equipment Manufacturing Conference, Sept. 9-11, 1985, Philadelphia, PA.

4. Luke, P. and A.V. Olver. "A study of churning losses in dip-lubricated spur gears," Proceedings of the Institution of Mechanical Engineers, Part G, Vol. 213, 1999, pp. 337-346.

5. British Standards Institution, BS ISO/TR 14179:2001(E), Gears--Thermal Capacity, BSI, London, United Kingdom, 2001.

6. Wu, S., and H.S. Cheng, "A friction model of partial-EHL contacts and its application to power loss in spur gears," Tribology Transaction, Vol. 34, Part 3, 1991, pp. 398-407.

7. American Gear Manufacturers Association, AGMA Standard 218.01, Rating the pitting resistance and bending strength of spur and helical involute gear teeth, AGMA, Alexandria, VA, December 1982.

Petra Heingartner is a Textron Six Sigma black belt for fluid and power at Textron Fluid & Power, located in Huddersfield, England. She leads cross-functional teams to improve work processes throughout the business. Previously, she was a senior design engineer and a senior applications engineer of Textron’s custom-made heavy industrial gear units.

Dr. David Mba is senior lecturer and postgraduate course director in the automotive, mechanical and structures engineering department at Cranfield University, located in Cranfield, England. He is director of the master’s course "Design of Rotating Machines" and is responsible for its industrial collaborations and is director of the continued-professional-development course "Gear Design." He also leads the department’s machine diagnostics group, which is involved with consulting and doctoral research. Mba specializes in machine diagnostics, rotor dynamics and machine design. Also, he’s developing a research and experimental facility to predict nonload gear losses in worm gearboxes.

Nomenclature
Ag	Arrangement constant A g =0.2
C1	Constant,29.66
C2	Constant,9 ·10 7
D	Element diameter
FR	Rolling force
FS	Sliding force
Lc	Contact line length
PCL	Churning power loss
PR	Rolling power loss
PS	Sliding power loss
PWL	Windage power loss
Rf	Roughness factor
VS	Sliding velocity
VT	Rolling velocity
b	Face width
df	Root diameter
dk	Outside diameter
fg	Gear dip factor (Ratio of dipping depth to element outer diameter) fg = 1 element fully submerged
h	Isothermal central film thickness
mn	Normal module
n	Rotational speed
w	Load parameter
wn	Normal gear contact load
Β	Helix angle
λ	Gearbox space function
μ	Coefficient of friction
μ0	Ambient viscosity at ambient temperature
v	Kinematic viscosity at operating temperature
φ	Oil mixture function,φ =1 oil-free atmosphere
φt	Thermal reduction factor
Subscripts
i	Element under consideration

Appendix A--Gear Data
			Units
Pinion teeth number	z1	115	--
Wheel teeth number	z2	21	--
Center distance	a	609.6	mm
Normal module	m	8 mm
Normal pressure angle	α	20	deg.
Helix angle	Β	25	deg.
Face width	b	285.75	mm	Double helical
Pinion shift coefficient	x1	0.989	--
Wheel shift coefficient	x2	0.181	--
Pinion, Young’s modulus	E1	207,000	N/mm 2
Wheel, Young’s modulus	E2	207,000	N/mm 2
Pinion, Poisson’s ratio	ny1	0.3
Wheel, Poisson’s ratio	ny2	0.3
Specific heat	C1	544	J/kgK
Specific heat	C2	544	J/kgK
Thermal conductivity	K1	46	W/mK
Thermal conductivity	K2	46	W/mK
Application
Pinion speed	n1	1,460	rpm
Transmitted power	P	8,952	kW
Lubricant
Lubricant factor	--	1		for mineral oil
Viscosity	ny	46	mm 2 /s	at 313 deg. K
	ny	21	mm 2 /s	at 333 deg.K
Specific gravity	ρ	873	kg/m 3
Dynamic viscosity	η	0.01833	Pa*s
Viscosity-pressure coefficient	α	2.20E-08	m 2/N
Thermal conductivity	Kf	1.25E-01	W/(m*K)

Appendix A--Calculated Gear Data
Contact line length	L c	mm	499.57
Operating diameter speed	v	mm/s	78,811
Gear contact tangential load	W pt	N	113,588.59
Gear contact normal load	W pn	N	133,374.62
Equivalent Young’s modulus	E eq	N/mm 2	227,472.53
Pinion torque	T 1	Nm	58,551.58

Appendix B--Bearing, Lubrication Pump and Seal Losses
Power input (kW)	8,952	6,714	4,476	2,238
%load	100%	75%	50%	25%
Experimental total loss (kW)	125.33	116.82	112.35	106.75
Power Loss in Each Bearing
Pinion coupling bearing (kW)	22.9	21.37	19.37	17.28
Pinion tail bearing (kW)	22.9	21.37	19.37	17.28
Wheel coupling bearing (kW)	3.93	3.67	3.43	3.09
Wheel tail bearing (kW)	3.93	3.67	3.43	3.09
Lubrication Pump
Absorbed power (kW)	16.59	16.59	16.59	16.59
Seal Losses at Each Shaft (kW)
Pinion coupling (kW)	0	0	0	0
Wheel coupling (kW)	0	0	0	0
Total loss (kW)	70.25	66.67	62.19	57.33