Impact of Indexing Errors on Spur Gear Dynamics
Impact of Indexing Errors on Spur Gear Dynamics
Murat Inalpolat, Michael Handschuh and Ahmet Kahraman
A transverse-torsional dynamic model of a spur gear pair is employed to investigate the influence of gear tooth indexing errors on the dynamic response. With measured long-period quasi-static transmission error time traces as the primary excitation, the model predicts frequency-domain dynamic mesh force and dynamic transmission error spectra. The dynamic responses due to both deterministic and random tooth indexing errors are predicted.
Introduction
Every manufactured gear contains certain types and magnitudes of errors depending on the quality level imposed. Such errors often contribute to the loaded transmission error to affect the meshing dynamics of gears. Consequently, understanding the impact of different gear design and manufacturing based errors and tolerances on the dynamic transmission error of gears is crucial. One of the most significant contributors to the gear transmission error is the tooth indexing errors. Gear tooth indexing error (deviation) is defined as the displacement of any tooth flank from its theoretical position relative to a reference tooth flank (Ref. 1). In relation to it, tooth spacing error is defined as the circumferential position error of one gear tooth flank with respect to the previous tooth flank. Ideally, a particular gear with Z number of teeth has identical involute profiles equally spaced around the pitch diameter. Existence of indexing error means that some of the tooth profiles are angularly misplaced from their ideal position with respect to one randomly chosen reference profile (index tooth or profile), say Tooth-1 without loss of generality. The right-hand side flank of Tooth- 1 is the reference profile (flank) when certain amount of torque acting in the clockwise direction is assumed to exist on this gear. The circular distances, S1 and S2, between the right flanks of Tooth-1 and Tooth-2, and also between Tooth-2 and Tooth- 3, where both flanks intersect the reference diameter, are both equal to a circular pitch p (p = πm, where m is the module) for a gear with ideal geometry. If S1 deviates from the nominal circular pitch p (S1 ≠ p), then the difference is interpreted as the spacing error ε1 for Tooth-2. Similarly, if S2 has a different value than p, then it is interpreted as the spacing error ε2 for Tooth-3. The value ε1 + ε2 will then be the indexing error for Tooth-3. If spacing error of any Tooth-N is εN-1 on a gear, then the corresponding indexing error for Tooth-N will be ΣN-1 j=1, where j is the indexing error index.
Gear tooth indexing errors arise during manufacturing, causing deviations related to the cutting or heat treatment process in addition to the random components (Ref. 2). Indexing errors modify the transmission error as they cause a certain gear tooth profile to be misplaced on the reference diameter, thus either coming into contact earlier or later with the corresponding tooth on the other gear in mesh compared to its expected timing under ideal conditions. This essentially shifts the contact in time that can significantly change the dynamic behavior of the gears, as the dynamic excitation phase continuously changes and instantaneous contact ratio becomes lower or higher than expected at different times, causing either overloading or contact loss of the tooth in mesh. Consequently, complicated indexing error patterns that interact with each other on gears in mesh could significantly alter the resultant life of gears under operation. The frequency spectra for the gears with indexing error show significant increase to the non-harmonic orders, making the spectra broad-band (Ref. 3).
The main reason for these non-harmonic orders to exist is the non-periodic transmission error values due to spacing/indexing errors. Therefore, it is not sufficient to use limited Fourier series amplitudes of transmission error to simulate the meshing dynamics anymore. The proper means of simulating indexing errors would be to apply the errors over multiple revolutions of both pinion and gear, covering their total hunting period. Worst-case spacing errors occur when the respective errors of the pinion and gear match up.
Bulk surface temperature. When the pinion and wheel are running under a given load, the surfaces of the pinion and wheel teeth are heated by the sliding friction between the gear teeth and gradually increase in temperature until finally reaching the equilibrium bulk surface temperatures after many revolutions.
The published work on the effects of indexing errors on gear dynamics is rather sparse. Remmers (Ref. 2) developed an analytical method to study the effect of tooth spacing errors, load, contact ratio and profile modifications on the gear mesh excitations. He indicated that random tooth spacing errors may be used to reduce the gear mesh excitations at certain frequencies. Mark (Refs. 3–4) derived expressions for Fourier series coefficients of all components of static transmission error, including harmonic and non-harmonic coefficients of gear defects of concern. He used two-dimensional Fourier transforms of local tooth pair stiffness and tooth surface deviations from perfect involute to come up with these expressions and used them to study mesh transfer functions of gears with different surface and profile deviations. Kohler and Regan and later Mark (Refs. 5–7) discussed components of the frequency spectrum for gears with pitch errors based on analytical approaches and agreed on the fact that existence of the components depends on loading conditions, and if the only deviation from perfect tooth geometry is due to pitch errors, then frequency spectrum of corresponding transmission error function will have no components at the mesh frequency harmonics. Padmasolala et al. (Ref. 8) developed a model to understand the effectiveness of profile modification for reducing dynamic loads in gears with different tooth spacing errors. They showed that linear tip relief is more effective in reducing dynamic loads on gears with relatively small spacing errors, whereas parabolic tip relief becomes more effective when the amplitude of the spacing error increases. Wijaya (Ref. 9) studied the effects of spacing errors and run-out on the dynamic load factor and the dynamic root stress factor of an idler gear system. He employed an analytical approach that defines the static transmission error and static tooth forces and predicted dynamic mesh force spectra of an idler gear system using a linear, time-invariant model. Spitas and Spitas (Ref. 10) also investigated overloading of gears and effect of tip relief on the dynamics of gears with indexing errors. They employed a geometry-based meshing analysis with a multi-degree-of-freedom dynamic model and reported simulated load factors and transmission error functions for gears with assumed indexing errors. Milliren (Ref. 11) and Handschuh (Ref. 12) investigated the influence of various gear errors on the quasi-static transmission errors and root stresses of spur gears experimentally. They used the same test rig to investigate the effects, such as spacing errors and lead wobble on the transmission error. Moreover, they compared experimental results with the results of a contact model and showed that the results are highly correlated.
In this study, the impact of indexing errors on dynamics of spur gears is investigated. A test setup and its encoder-based measurement system are used to measure loaded transmission error excitations. A dynamic model capable of including long-period transmission error excitations is proposed to demonstrate the effect of indexing errors on the resultant dynamics of gears.
Dynamic Model Formulation
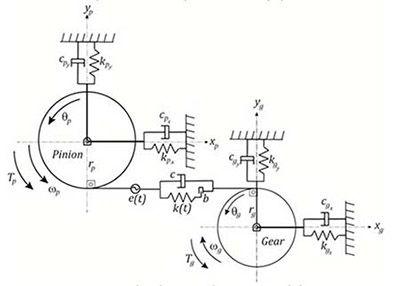
In this study, impact of indexing errors on spur gear dynamics is demonstrated via a simplified lumped parameter dynamic model, as shown in Figure 1. It is a 6 degree-of-freedom (DOF) dynamic model that assumes both gears can translate in x and y coordinates and also can rotate about their own local rotational axis represented by the z coordinates. However, the line of action (LOA) is selected such that it is coincident with the global x-axis of the inertial frame which uncouples the gear dynamics observed in the y directions for both gears from the rest. Consequently, the model can essentially be seen as a 4 DOF gear pair model that represents the LOA and torsional dynamics, as shown by several other researchers to be a valid model when not including the effects of friction (Refs. 13–15).
The proposed model can accept broadband quasi-static transmission error excitations both in the form of long-period time domain input and also in the form of multi-harmonic frequency domain input. This is shown to be superior when certain timevarying and nonlinear effects act on the dynamics of the gear pair simultaneously, such as the cyclo-stationary, quasi-static transmission error.
In the lumped parameter dynamic model developed here, gears are represented by rigid disks which are connected to each other through a number of elements. A spring element is used to represent gear mesh flexibility k(t), which is a time-varying function that is evaluated at different input torque levels by using a contact model (Ref. 16). Here, k(t) includes the parametric excitations due to the mesh stiffness variation caused by the fluctuation of number of teeth in contact into account. A clearance element b accompanies the mesh stiffness function to account for tooth separations caused by backlash or other tooth profile deviations. A viscous damper element c is employed to represent the gear mesh energy losses. A displacement element e(t) is used to represent the quasi-static transmission error that acts along the line of action. The quasi-static transmission error function is also load-dependent and thus should be evaluated at each different input torque level.
Each disk that represents a gear body has a mass of mi, a mass moment of inertia of Ji and a base radius of ri, where i = p or g. Gear bodies are supported by stiffnesses kix, kiy, and also by dampers cix, ciy, which represent the combined elasticity and damping of supporting bearings and shafts that carry the gears. The equations of motion are given below where xi, yi are the translational, and θi are the rotational degrees-of-freedom for the gear bodies:
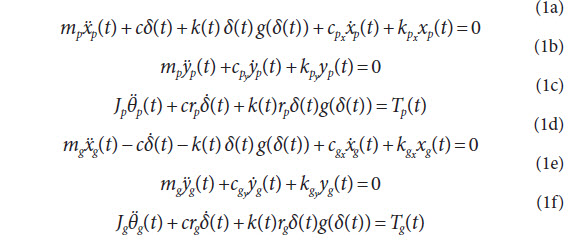
In Equation 1 a-f, δt represents the relative mesh deflections defined as:
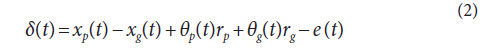
and gear mesh contact loss is mathematically induced by the unit step function, g(δ(t)). The unit step function, g(δ(t)) = 0, if δ(t) < 0 and g(δ(t)) = 1, if δ(t) ≥ 0. An over-dot means a time derivative of the corresponding variable in the equations of motion. In Equation 2 e(t) is the time-varying transmission error function that represents the motion errors caused by gear mesh deflections due to load and also due to manufacturing deviations. Transmission error is a periodic function and is simulated via discrete Fourier series amplitude and phase of this periodic function in modeling schemes that exist in literature (Refs. 16–17). The model can employ the transmission error function either in a time-series form or in a broad-band frequency domain form from a measured or a simulated timeseries. In other words, this model makes it possible to use measured time-domain or broad-band frequency domain representation of the long-period quasi-static transmission error to predict dynamic transmission errors and dynamic mesh forces. Moreover, the dynamic model developed in this study accepts measured transmission error signal with any resolution, automatically synchronizing the time resolution of the transmission error signal with the time resolution of the dynamic model equations for the right solution. A simplified mathematical representation of such a signal in the time domain can be given as:
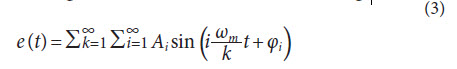
This transmission error function assumes an infinite number of harmonics, sub-harmonics and overtones of the mesh frequency ωm that are superimposed to obtain a broadband transmission error function as in Equation 3. The quasi-static transmission error, e(t), when measured from a gear set with indexing errors, is periodic over the complete rotation of the gears in mesh if the gears are unity-ratio gears. If two gears with different number of teeth are used, then transmission error signal is periodic over Z1Z2 rotations of both gears, where Z1 and Z2 represent the number of teeth on the pinion and the gear, respectively. On the contrary, for a gear set with no indexing errors, transmission error is periodic over a mesh cycle and over a complete rotation of the gear. This difference constitutes the main mechanism for the signals to convolute.
This dynamic model employs a number of assumptions. First of all, gear wheels are assumed to be rigid, with flexibility only coming from the gear mesh. Gear motions in some other directions, such as rotations about x and y, and translations in z, are excluded for the sake of simplicity. Bearings are assumed to be linear. Finally, simplified damping elements are used. The model presented here makes use of Rayleigh damping, where [C] = α [M] + β [K]. Here, [C], [M] and [K] represent the overall system damping, mass and stiffness matrices and αand β are constant coefficients, and α = 479 and β = 1.4·10-7 was used here.
Experimental Transmission Error Measurements
Test machine and set-up. In this study, an open-architecture gearbox with drive and load capacity was used to measure the quasi-static transmission error of spur gears with different indexing errors. This rig (Fig. 2) is designed to operate gears under high-load and low-speed (loaded quasi-static) conditions. A small DC motor is connected to a 100:1 ratio harmonic drive to reduce the speed significantly while increasing the torque delivered to the gear pair. The harmonic drive was directly connected to a torque-meter to monitor the input torque provided to the gearbox. The output side of the torque-meter was connected to one of the test gear shafts via a flexible elastomer coupling. The test gearbox consisted of a unity-ratio spur gear pair held by relatively rigid shafts. Concentric bearing housings holding the bearings were mounted on two massive split pedestals. The shaft of the driven (output) gear was connected to a magnetic particle brake with a maximum torque capacity of 400 Nm by means of another flexible coupling. The shafting permitted optical rotary encoders to be mounted on their free ends outside the bearing pedestal for measurement of TE. The rotary encoders (Heidenhain, RON 287) have the capability to measure 18,000 positions per complete rotation.
Test specimens and test matrix. Unity-ratio spur gear pairs were used in this study with an operating center distance of 150 mm. A total of 7 gears with tightly controlled indexing errors formed the inventory for the test matrix. Two gears with no indexing errors, three test gears with discrete spacing errors at a few teeth along with two additional gears with randomized spacing errors were procured specifically for this study. Basic gear parameters for these gears are listed in Table 1. Each gear pair had a theoretical contact ratio of 1.8. The test gears had the following intentional spacing errors:
- Gears #1, #2: Gears with no indexing errors (in reality, errors exist but less than 2 μm).
- Gear #3: Gear with a single tooth having a negative 15 μm spacing error.
- Gear #4: Gear with two consecutive teeth having negative 15 μm spacing errors.
- Gear #5: Gear with two teeth having negative 15 μm indexing errors with the tooth in between them in the correct position.
- Gears #6, #7: Gears with all teeth having spacing errors with randomly distributed magnitudes between the range [-15, 15] μm.

Each error was placed in the negative direction, which refers to the tooth entering mesh later than expected. The negative direction of the errors was chosen because they were obtained by removing additional material from the teeth with no error. Likewise, if a tooth enters mesh earlier than nominal compared to the previous tooth, the spacing error is positive. Moreover, a more realistic case where two gears having various different indexing errors was studied utilizing the gears designated as Gears #6 and #7. These gears were machined to have random spacing errors within the range [-15, 15] μm. Furthermore, with right and left flanks having different error values, these two gears represented four different random spacing error conditions.
Transmission error measurements. The transmission error measurement system used two separate encoders to determine the angular position of each gear shaft. The signals from the encoders were passed into encoder conditioners. A commercially available transmission error measurement system was used to process the conditioned encoder signals to compute the transmission error. The software has high and low pass filtered TE time histories of the same data to quantify shaft and mesh frequency content of the TE signal. This system considers either the driving pinion (input) encoder or the driven gear (output) encoder as the reference signal to determine output and input TE signals (both in μrad), or as a linear displacement along the line of action as:
These TE measurements are processed using data segments corresponding to 16 complete gear rotations. In Figure 3 a representative measured loaded e(t) is presented from Test #2 at 200 Nm. In Figure 3 (a, b), the unfiltered (raw) and the high-pass filtered versions of the measured e(t) is presented. Although the measurements were recorded for 16 complete gear rotations, only one complete rotation, including 50 gear mesh cycles, is presented in these figures. These representative measurements clearly exhibit the intentional indexing error amount generated on the test gears. With the gear rotational speed of 10 rpm, gear mesh frequency is 8.33 Hz. Accordingly, the measured TE signal is put through a high-pass filter with a cut-off frequency slightly higher than 0.167 Hz, removing frequencies equivalent to one shaft order frequency and below. A family of baseline tests of the two no-error gears was run first at all of the operating conditions specified. The sinusoidal waviness in Figure 3(a) is the once-per-revolution amplitude caused by the pitch line run-out error of the gear pair. Once such low-frequency content is removed by the high-pass filter, the remaining TE is seen to be dominated by the gear mesh orders (50, 100, 150, etc.), and the resultant TE time histories reveal mesh frequency components of TE. It is also observed from the filtered data that certain tooth-to-tooth variations exist. This is a direct result of a small amount of spacing errors present in these noerror gears — despite all efforts to minimize them. As a result, the frequency spectrum has other non-zero, non-mesh harmonics — especially below the fundamental gear mesh order of 50.
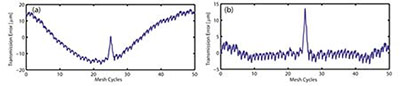
Figure 3 Measured static TE from Test #2: (a) unfiltered TE; (b) filtered TE.
- Click image to enlarge
Results and Discussion
In this section, impact of indexing errors on dynamic response of gear pairs is presented utilizing predicted dynamic transmission error time histories and corresponding frequency spectra. Dynamic transmission error (DTE) predictions are compared to the baseline measured quasi-static transmission error e(t) time histories (STE) and frequency spectra of the corresponding gear pairs. Here results are reported in terms of dynamic transmission error, as it provides the most direct physical link between the measured STE and predicted DTE while the model is also capable of predicting dynamic mesh force, dynamic bearing forces and displacements and gear motions, as defined in all 6 degrees of freedom.
First, a linear time-invariant (LTI) version of the same dynamic model was run to determine the resonant frequencies and corresponding mode shapes of the baseline gear pair with no indexing errors. The resonant frequencies were found to be at 3,370, 5,940 and 7,300 rpm. As pointed out earlier, dynamics regarding the y-direction motions were excluded from the discussion, as they can be treated independently. Later, dynamic response and mesh force spectra of the same baseline gear pair were predicted utilizing both LTI and NTV versions of the model to identify the off-resonant speed (frequency) ranges of the system within which specific frequencies were chosen for further analysis. The off-resonant frequencies that were used for further analysis are 400 rpm, 1,300 rpm and 2,100 rpm. At these off-resonance speeds, magnification on the TE due to the gear pair dynamics can be clearly observed without the extra amplifications due to mesh resonances and nonlinear effects.
Although numerous test cases, along with the corresponding dynamic model predictions, were carried out, a subset of the results is reported here to illustrate the importance of incorporating indexing errors into the gear design and dynamics considerations. Results from Test #1 that included the baseline gears with no indexing errors along with the corresponding dynamic transmission error predictions are shown in Figure 4.
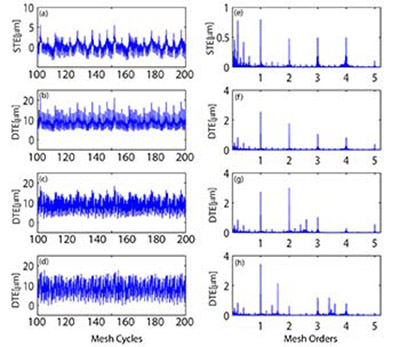
Figure 4 Measured static TE (a) along with predicted dynamic TE time histories from Test#1 at 400,
1,300 and 2,100 rpm (b-d); and corresponding frequency spectra (e-h).
- Click image to enlarge
In Figure 4(a) a measured STE time history is given between gear mesh cycles 100 to 200. This mesh cycle range was intentionally chosen to exclude any transient effects taking place — especially for the initial cycles for the predicted DTE. In addition, measured STE and predicted DTE traces were presented within the same mesh cycle ranges to clearly demonstrate the dynamic magnification effects. It is apparent from both Figure 4(a), and its corresponding frequency spectrum Figure 4(e), that even baseline gears had limited indexing errors on them along with teeth deflection and other geometric imperfections that contributed to the STE. Predicted DTE at 400 rpm, 1,300 rpm and 2,100 rpm is presented in Figure 4(b-d), along with their corresponding frequency spectra in Figure 4(f-h). Although it is clearly observed from the comparison between time histories for STE and DTE at different speeds how dynamics play a significant role on TE, note also that frequency spectra are intentionally presented in gear mesh orders to help us detect the changes at main mesh order and its harmonics, shaft orders and also gear pair resonances at once. For instance, in Figure 4(g), when gears were rotating at 1,300 rpm, resonant peak revealed at the mesh order 2.8 that corresponded to the second mode (torsional mode) of the system. Similarly, in Figure 4(h), when gears were rotating at 2,100 rpm, resonant peaks at the mesh orders 1.6 (torsional mode) and 3.6 (coupled torsional-translational mode) were revealed due to gear pair dynamics.
In Figure 5 STE and DTE time histories, and corresponding frequency spectra from Test #2, are given following the same sequence in Figure 4. Test #2 included a gear with no indexing errors and a pinion with an intentional spacing error of 15 μm at tooth #25 (Fig. 3). The peaks that are seen in the filtered STE time trace (Fig. 5(a)) exhibit how the discrete spacing error of the particular tooth on the gear comes in mesh and causes a sudden increase in the measured STE once during a complete rotation of the gear; i.e. — once in every 50 mesh cycles. The fact that one of the teeth has discrete spacing error, whereas all the other teeth have almost perfect spacing, breaks the cyclo-symmetricity of the meshing action and thus mistunes the dynamics of the gear pair. This can essentially be observed in Figure 5(a-d), when the same gear pair was used but was run at sequentially increasing speeds. Especially, in Figure 5(c) and (d), when the gears were rotating at 1,300 and 2,100 rpm, respectively, time traces exhibit how more than once mesh cycle was affected due to a single discrete spacing error on the gear.
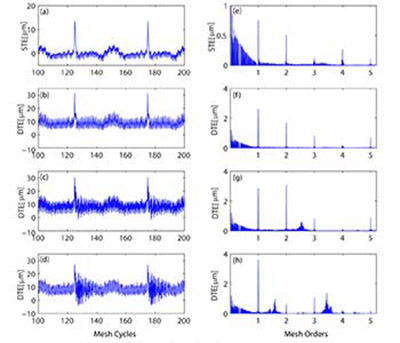
Figure 5 Measured static TE (a) along with predicted dynamic TE time histories from Test #2 at
400, 1,300 and 2,100 rpm (b-d); and corresponding frequency spectra (e-h).
- Click image to enlarge
Under dynamic conditions, teeth do not only deflect due to the applied external load, but also oscillate about this pre-deflected position under the influence of dynamic loads. Moreover, indexing errors cause time and phase lags (or leads) on the mesh timing that can cause dynamic loads to become magnified and also modify them to where they become more impulsive. Gear contact ratio reinvigorates the gear pair dynamics as it is the most important design parameter that decides upon when and how much load will a particular tooth carry. Moreover, mesh damping strongly influences the dynamic response of the gears, but is hard to determine and also to change. The other important point to stress here is the energized broad-band shaft order regime and its physical reasoning. In Figure 5(e-h), although run-out effects were excluded from the measured STE, shaft order (orders lower than the fundamental mesh order) peaks and integer multiples are revealed. The main reason is that the teeth with deterministic spacing error repeats and leaves its signature once in every rotation of the gear, leaving a strong mark on the frequency spectrum. This effect becomes even more significant when dynamics come into play at higher speeds. The peaks revealed at integer multiples of the shaft orders are due to the amplitude and phase modulation of the TE and will be further studied in a subsequent study by the authors. In Figure 6, results from Test #3, where an intentional deterministic indexing error pattern of 0-15-0-15-0 μm was used on the pinion, is presented. In this case there is a single, intentionally misplaced tooth on the gear that was followed by both a perfectly positioned and misplaced tooth. This error pattern introduced another layer of complications to the resulting frequency spectra by strengthening 2× shaft orders along with 1× shaft orders. The complicated phasing relationship affected the resulting peak distribution in the frequency spectra, which is more clearly visible from orders lower than the fundamental (1×) gear mesh order.
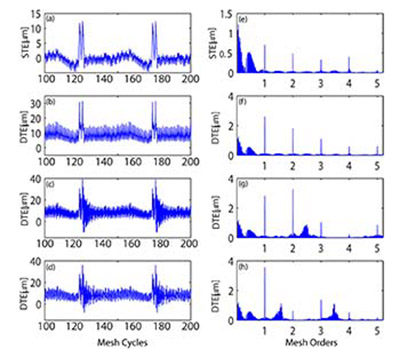
Figure 6 Measured static TE (a) along with predicted dynamic TE time histories from Test #3 at
400, 1,300 and 2,100 rpm (b-d); and corresponding frequency spectra (e-h).
- Click image to enlarge
The measured STE and predicted DTE thus far have included intentionally created, deterministic indexing errors on the gear. In Figure 7, however, results from Test #4, which included random spacing errors on the pinion, are presented. The random error pattern is definitely more representative of the real indexing error patterns observed on the gears manufactured using cutting, shaping etc. operations. Although randomly distributed, spacing errors were kept between the range [-15, 15] μm. As seen both from the time traces and the corresponding spectra (Fig. 7), random spacing error patterns cause a truly broadband excitation, thereby activating the resonant peaks and shaft orders — regardless of gear speeds.
Conclusions
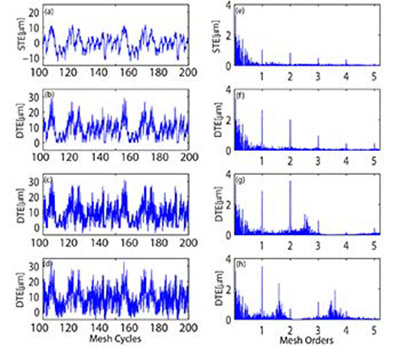
Figure 7 Measured static TE (a) along with predicted dynamic TE time histories from Test #4 at 400,
1,300 and 2,100 rpm (b-d); and corresponding frequency spectra (e-h)
- Click image to enlarge
In this study a model to predict gear pair dynamics using measured, long-period quasi-static transmission error of a gear pair was developed. This model uses measured, broadband static TE excitation with any time and frequency resolution and predicts dynamic gear mesh force, dynamic TE and bearing forces. Both time domain and frequency domain results can be obtained at steady-state and transient speed conditions. First, gears were intentionally mistuned through tightly-controlled deterministic and stochastic indexing errors, and resulting gear pair dynamics were compared against a baseline gear pair with no indexing errors (minimized, but not zero). Cases with gears having limited, discrete indexing errors increase the dynamic response during a limited number of mesh cycles, thus increasing the dynamic response. Their frequency spectra are enriched by additional shaft order peaks due to amplitude and frequency modulations caused by the perturbed transmission error excitation. Cases with random indexing error exhibit even greater broadband response, having peaks at shaft order and its integer multiples along with mesh order and its harmonics. They exhibit significantly more energy content at frequencies lower than the fundamental mesh frequency. The broader spectrum is caused by the broadband TE excitation causing a frequency modulated dynamic mesh force spectrum.
References
- AGMA Technical Standards. ANSI/AGMA 2015-1-A01.
- Remmers, E.P. “Gear Mesh Excitation Spectra for Arbitrary Tooth Spacing Errors, Load and Design Contact Ratio,” J. of Mech. Des.100, 1978, 715–722.
- Mark, W.D. “Analysis of the Vibratory Excitation of Gear Systems, Part I: Basic Theory,” J. Acoust. Soc. Am. 63 (5), 1978, 1409–1430.
- Mark, W.D. “Analysis of the Vibratory Excitation of Gear Systems, Part II: Tooth Error Representations, Approximations, and Application,” J. Acoust. Soc. Am. 66 (6), 1979, 1758–1787.
- Kohler, H. and R. Regan. “The Derivation of Gear Transmission Error from Pitch Error Records,” J. Mech. Eng. Science, 199 (C3), 1985, 195–201.
- Mark, W.D. “The Role of the Discrete Fourier Transform in the Contribution to Gear Transmission Error Spectra from Tooth Spacing Errors,” J. Mech. Eng. Science, 201(C3), 1987, 227–229.
- Kohler, H., R. Regan and W. D. Mark. “The Derivation of Gear Transmission Error from Pitch Error Records,” Discussion, J. Mech. Eng. Science, 201(C3), 1987, 230–232.
- Padmasolala, G., H. H. Lin and F. B. Oswald. “Influence of Tooth Spacing Error on Gears With and Without Profile Modifications,” NASA/TM 2000- 210061 PTG-14436, October 2000.
- Wijaya, H. “Effect of Spacing Errors and Runout on Transverse Load Sharing and Dynamic Factors and Idler Gear Dynamic Analysis,” MS Thesis, The Ohio State University, Columbus, Ohio, 2001.
- Spitas, C. and V. Spitas. “Calculation of Overloads Induced by Indexing Errors in Spur Gearboxes Using Multi-Degree-of-Freedom Dynamical Simulation,” J. Multi-Body Dynamics 220, 2006, 273–282.
- Milliren, M. “An Experimental Investigation Into the Various Errors on the Transmission Error and Root Stresses of Spur Gears,” MS Thesis, The Ohio State University, Ohio, 2011.
- Handschuh, M. An Investigation into the Impact of Random Spacing Errors on Static Transmission Error and Root Stresses of Spur Gear Pairs,” MS Thesis, The Ohio State University, Ohio, 2013.
- Tamminnana, V.K., A. Kahraman and S. Vijayakar. “On the Relationship between the Dynamic Factors and Dynamic Transmission Error of Spur Gear Pairs,” J. Mech. Des., 129, 2007, 75–84.
- Kahraman, A., J. Lim and H. Ding. “A Dynamic Model of a Spur Gear Pair with Friction,” 12th IFToMM World Congress, Besançon (France), June 18–21, 2007.
- Blankenship, G. W. and A. Kahraman. “Steady State Forced Response of a Mechanical Oscillator with Combined Parametric Excitation and Clearance Type Nonlinearity,” J.Sound and Vibr., 185, 1995, 743–765.
- Windows LDP. The Ohio State University, Columbus, Ohio, 2013.
- External2D. Advanced Numerical Solutions, Inc., Hilliard, Ohio, 2013.