Management Summary
Due to its high economical efficiency, the gear shaving process is a widely used process for soft finishing of gears in the gear manufacturing industry. However, because of highly increased efficiency, other gear finishing processes, especially gear hobbing, have recently become competitive with the shaving process for soft finishing of gears.

In contrast to other machining processes with geometrically defined cutting edges, the gear shaving process has been improved little during the past 30 years. So far, it is not known if the machining parameters in gear shaving represent an optimum as they are or if there is a potential for further optimization. Therefore, in this report, different approaches to increase the tool life and the productivity are discussed, using different simulation techniques.

At first, a geometrical simulation tool based on penetration calculation is used in order to analyze the geometrical and kinematical conditions of the gear shaving process. The information gained by this type of analysis is used to create another simulation model which is based on FEA. This two-dimensional model allows the determination of physical values like stresses, forces, temperatures and others. Also, with this type of simulation, it is possible to determine the effect of tool wear on the chip creation process.

The information gained with the two different simulation techniques is subsequently used to find different approaches to optimize the gear shaving process.

Introduction and Objective
With the gear shaving process, it is possible to create good gear quality with low machining costs and high process reliability. This has lead to a wide industrial application of this proc-ess for soft finishing of gears. However, this high economic efficiency has prevented further improvements in gear shaving during the recent decades. Due to the high reliability and economic efficiency, it was not considered necessary to improve the process.

In contrast to this, the productivity of other gear manufacturing processes has dramatically improved, especially during recent years. The reason for this can be seen in a high technological understanding of those processes. In gear hobbing, for example, productivity has been improved by about 800% during the last 30 years, making this process even competitive with gear shaving for soft finishing, despite fundamental theoretical disadvantages. At the same time, hard finishing processes like grinding or honing have also been improved so that, considering the higher achievable gear quality, these processes appear to be another viable alternative.

However, all other gear finishing processes—gear hobbing, grinding as well as honing—have to be driven at their technological limits, whereas in gear shaving, the process appears to be far from its possible limits. The applied cutting speeds are in the range of 20–60 m/min and the chip thicknesses are also very low.

Since gear shaving as a soft gear finishing process has various specific advantages against other gear finishing processes in many areas, there is a need for further improvement of the gear shaving process in terms of economic efficiency and quality. New machine concepts have been developed to fulfill this requirement, but in industrial practice, the increase of the process, in many cases, has not been achieved.

Therefore, this report will analyze by what means the costs of the gear shaving process can be decreased. This includes an analysis of the different types of costs in gear shaving and the creating of strategies to reduce the machining costs. For this, different types of simulation techniques will be used. The geometry of the cut and the process strategy can be analyzed using penetration calculation, while the effects on the chip creation and the process forces can be determined using an FEA-based process simulation model. The combination of both simulation techniques allows a detailed analysis of the gear shaving process, considering the technological peculiarities of the process, without costly and time-consuming machining trials.

State of the Art
Fundamentals of gear shaving. Gear shaving is a soft finishing process for gears using a geometrically defined cutting edge. The kinematics are identical to a non-parallel-axis gear drive. The tool is a gear with radial-interrupted flanks and with a different helix angle than the workpiece (see Fig. 1). The tool and the workpiece axis are therefore not parallel, which creates the so-called crossed-axis angle S. In industrial practice, the values for this crossed-axis angle range between 10–15°. In some exceptions, crossed-axis angles between 2–20° can be applied (Ref. 1).

Figure 1--Principle of gear shaving.

The chip creation is accomplished by moving the workpiece and the gear radially together with high force while they are rolling up on each other. Usually, the tool is driven by the machine, while the workpiece is following freely. Due to the crossed-axis angle, an axial relative movement is created, and due to the penetration of the cutting edges and the gear flank, chips can be created (Ref. 2).

Since the flanks of the tool are radially interrupted in order to create the cutting edges, but there is no modification of the flanks, the constructive clearance angle is 0°. When the cutting edge is approaching the workpiece flank, even negative clearance angles are created, leading to a plastic deformation of the workpiece flank underneath the tool flank. This effect is desired in gear shaving since it leads to an elimination of the feed scallops of the machined surface, creating a good surface quality (Ref. 3). Due to this combination of machining and deforming, the gear shaving process is a machining process which shows various technological peculiarities compared with other machining processes with geometrically defined cutting edges. Therefore, research results accomplished in other manufacturing processes cannot be transferred to the gear shaving process.

Analogous process for gear shaving. One reason for stagnating development of the gear shaving process can be seen in the high expenditures necessary to perform systematic technological studies as well as in the very difficult analysis of tool wear on shaving wheels. A way to avoid these problems is via an analogous process for gear shaving, developed at WZL, which allows for a dramatic reduction of the expenditures for wear trials, while at the same time, much improving the accessibility of the cutting edge.

The aim of the analogous process is to reproduce the kinematic and geometrical contact conditions of the real gear shaving process as exactly as possible and thereby to create similar tool wear as in real gear shaving, considering the technological peculiarities of the process. Figure 2 shows the idea of this analogous process.

Figure 2--Analogous process for gear shaving.

The left part of the figure shows a shaving wheel meshing with a gear. In the contact point, the two parts have different curvature radii, which can be calculated for each contact point. These radii are transferred to cylindrical parts in the analogous process. Like in the real gear shaving process, these two parts roll up on each other, and the two axes are crossed. By means of the crossed-axis angle, an axial cutting speed of the cutter on the workpiece surface is created.

This way, it is possible to simulate different points of contact in the analogous process. The slip in profile direction, which also occurs during the real shaving process, can be simulated by varying the individual turning speeds of the two axes. The analogous tool represents a section out of a cylindrical part which has approximately the thickness of one serration on a real shaving wheel. There is only one cutting edge on the analogous tool, and this edge has a key angle of 90°. In contrast to real shaving wheels, it is possible with this very compact tool to study the wear using conventional or even scanning electron microscope photographs. The geometrical and kinematic conditions of the gear shaving process and the effects of different parameters on tool wear in gear shaving can thereby be studied independent of each other.

Possible conclusions about the tool wear in the analogous process are shown in Figure 3. In the lower left part of the figure, the development of tool wear over the tool life is displayed in different cross sections of the tool. These cross sections have been created using a tactile measuring device. It can be seen that during the whole tool life, a relatively sharp cutting edge is present with a radius of about 5 µm. At the same time, however, a chamfer on each side of the cutting edge is created. During the life time of the tool, this chamfer is continuously increasing (Ref. 4).

Figure 3--Tool wear and chip creation in the analagous process.

In industrial practice, tool wear in gear shaving is not determined by monitoring the shape of the cutting edge but by determining the quality of the machined gear. Likewise, in the analogous process, a way must be found to study the effect of tool wear on the ability of the cutting edge to create chips. A standardized quality measurement like for real gears cannot be performed. In the analogous process, however, it is possible to observe the chips created during the life time of the tool. Therefore, in the right part of Figure 3, chips that are created with a sharp tool are compared with chips created via a worn tool. It can be seen that there is a clear relation between tool wear and chip creation in gear shaving.

The measuring plot, displayed in Figure 3, allows the determination of different characteristic values to quantify the wear, such as the displacement of the cutting edge SV? and the wear mark VB. These values can be considered to be relevant for the chip creation since they are responsible for the amount of material that must be plastically deformed underneath the flank of the tool.

Economic efficiency of gear shaving. The analogous process described above has been used in previous studies (Ref. 1) in order to perform systematic wear studies of gear shaving. It could be shown in combination with trials in the real gear shaving process that dramatic improvements in productivity are possible when proper adaptations to the process are applied. A high increase in productivity results especially from eliminating the speed reversal in the shaving process while increasing the process and cutting speed.

One example for an optimized gear shaving process is displayed in Figure 4. It can be seen that by optimizing the process, a reduction of the machining time (tH) from 26 seconds to 12.5 seconds was achieved. That reduction is more than 50%. In the example, both the radial set-in per revolution and the axial feed were kept constant.

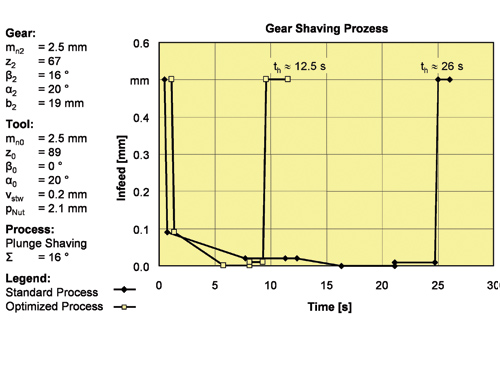
Figure 4--Comparison between optimized and state-of-the-art gear shaving process.

The machining costs are not only determined by the productivity of the process but also by the tool costs, which are nearly proportional to the tool wear. In order to study which of the two fields (productivity and tool costs) the highest costs are created, the machining costs for the processes described in Figure 4 are estimated in Figure 5.

Figure 5--Estimated machining costs.

The machine and labor costs are mainly determined by the cycle time, which consists of the machining time and the workpiece change time. The tool costs are determined by tool life, tool purchase costs and resharpening costs. The hourly costs for machine and worker have been estimated as accurately as possible, and the additional costs for maintenance, coolant, etc. were considered in separate hourly rates. The tool life has been estimated to about 1,500 parts per resharpening cycle for both machining processes, which is a realistic value according to the end-user. For the workpiece change, 15 seconds were estimated.

It can be seen in Figure 5 that for the state-of-the-art machining process, the machine and tool costs are on a similar level. Since the machine operator serves several machines at the same time, the labor costs are on a much lower level. By reducing the machining time by about 50%, the machining costs can only be reduced by about 15%. A further increase in productivity would cause an even lower reduction of machining costs. The reasons for this can be seen mainly in the constant workpiece change times, which cannot be improved by an increase in productivity, and in the constant tool costs. As a conclusion, it can be stated that in order to improve the economic efficiency of this process, the tool costs, and thereby the tool wear, must be reduced.

Geometrical Simulation of Gear Shaving by Penetration Calculation
As stated before, the gear shaving process is a very geometrically complex cutting process. In the past, it was not possible to determine the chip geometries in this process. By means of penetration calculation, however, a valuable tool is available to determine the geometries of the cuts and the chips (Ref. 4). The principle of this type of simulation is described in Figure 6.

Figure 6--Penetration calculation, simulation model.

In the left part of the figure, two teeth of a workpiece are displayed. Above them, the enveloping body of the cutting edge on its path through the gap can be seen. In the area in which the enveloping body and the gaps are penetrating, a chip is created. This area is better visible in the right part of the figure, in which not the whole teeth of the workpiece but only the flanks are displayed.

Since penetration calculation is a purely geometrical simulation, only an infinitesimally thin cutting edge is used. In contrast to that, in the real gear shaving process, the flanks of shaving cutters have an extension of about 1 mm. Underneath these flanks, material is plastically deformed. This influence cannot be considered in penetration calculation.

In Figure 7, an example for a simulation result of the penetration calculation is given. The left part of the figure shows a workpiece tooth with a single cut. The upper right part of the figure represents a three-dimensional picture of the cut in relation to the ideal involute. With this illustration, however, it is difficult to determine the actual geometry of the cut.

Figure 7--Example of simulation result.

In gear shaving, the cutting edges follow the gear profile and the cutting speed is perpendicular to this profile, so the cutting speed in gear shaving always points in the lead direction of the flank, despite the varying sliding velocities in the profile direction. Thus, the best analysis of the cutting edge track is possible in lead direction, displayed in the lower right part of Figure 7.

The diagram shows the flank in the lead direction after three cuts, which were performed according to a state-of-the-art plunge shaving process. Apart from the track of the cutting edge, the chip geometry (the hatched surface) can also be determined.

The simulation results can be used in order to create a model of the shaving process with realistic values for chip thickness and chip length, as shown in Figure 8. With this model, it is possible to estimate the actual loads on the cutting edge during the shaving process.

Figure 8--Chip geometries in gear shaving.

The figure shows the sequence of chips as created in a typical plunge shaving process. In this shaving strategy, the axis center distance is continuously reduced during the shaving operations. With this type of shaving process, the whole gear flank can be machined at once, so this is the most economical shaving process and therefore also the most popular one in industrial practice.

It can be seen in the figure that one cutting edge is exposed to a large number of different loads during the machining operation of one gear. While the cutting speed can be assumed to be almost constant during the whole machining operation, the chip thickness is changing significantly. At first, the chip thickness is constantly increasing as the axis center distance decreases until a constant level has been reached. In common plunge shaving processes, the value for the chip thickness is between 2–10 µm, depending on the feed rate and the gear data. When the final axis center distance is reached, the radial motion stops and the chip thickness decreases until the chip thickness falls below a critical value and no chips are created anymore. But not only the load on the cutting edge itself varies during one machining operation, the load on the tool flank (in other machining processes: clearance face) also varies strongly.

As a conclusion, it can be said that the shaving process differs in many ways from other machining processes with geometrically defined cutting edges. The main differences are (Ref. 1):

• negative clearance angles,

• very small chips (height: 50–150 µm; length: 100–400 µm),

• low thermal load on the cutting edge due to low cutting speeds and chip thicknesses, and

• strongly varying load on cutting edge and clearance face.

FE-Based Simulation of Gear Shaving
Starting in the recent past, FE-based machining process simulation has offered the opportunity to model machining processes and thereby to determine the loads on the tool depending on the previously mentioned boundary conditions of the gear shaving process. The penetration calculation model introduced above is used to determine the path of the tool through the workpiece surface and the workpiece geometry before the cut.

The FE-based simulation model used in the simulations described below is shown in Figure 9. Based on the previously determined path of the cutting edge, the path of the cutting edge in this simulation is approximated by a section of a circular curve, as shown in the upper middle part of Figure 9.

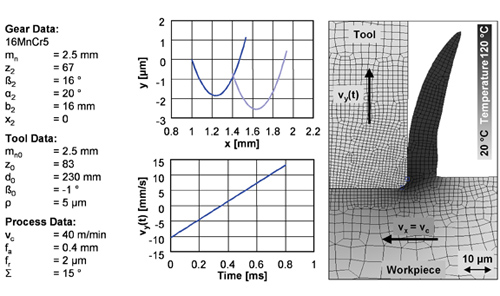
Figure 9--Model for FE-based simulation of plunge shaving.

From the path of the cutting edge during the cut, the velocity function in the y-direction can be determined, as shown in the lower middle part of the figure. The geometry of the workpiece before the cut is implemented by interpolation points. The material data (16MnCr5) is implemented in a specific material database with respect to the temperature as well as the strain rate. By using this simulation model, various physical values can be determined, i.e. stresses, temperatures, strain and strain rates (Ref. 5).

Simulation of parallel shaving. In order to obtain valuable simulation results by using the simulation model introduced above, it is necessary to verify this model. With a regular gear shaving process, it is not possible to verify simulation results because during a gear shaving cycle, many teeth and even more cutting edges are in use at the same time. Also, a large variety of different chip geometries is being generated, and neither temperatures nor cutting forces can be determined for a single cut in the real gear shaving process.

However, the analogous process introduced above can be used in order to verify the simulation model. Since only one cutting edge is in use at the same time, it is possible to observe the chip creation depending on the shape of the cutting edge, as displayed in Figure 3. Therefore, in Figure 10, three different cutting edge shapes have been used within a simulation model that corresponds to the geometrical conditions in the analogous process and a conventional parallel shaving process.

Figure 10--Simulation of chip creation in gear shaving.

In the upper part of the figure, the chip creation is displayed in the beginning of the cut (left) and close to the end of the cut (right) for a sharp tool with a cutting edge radius of about 5 µm. The stress within the workpiece surface is shaded dark. In the middle section of the figure, a worn cutting edge is simulated with a chamfer on each side of the cutting edge as shown in Figure 3. The bottom part of Figure 10 shows the chip creation when a cutting edge with a radius of about 20 µm is used without chamfers, as existent on coated cutting edges in gear shaving (Ref. 2).

It can be seen that there is a clear dependency of the chip geometry on the shape of the cutting edge. While, as in the analogous process, with a new cutting edge, thin and smooth chips can be created. With the worn and the coated cutting edges, the chips are much more deformed. With the worn cutting edge, nearly no chip creation is possible anymore. This could also be observed in Figure 3.

Simulation of plunge shaving. Due to its high economical efficiency, the plunge shaving process is by far the most commonly used gear shaving process in industrial practice (Ref. 3). With the analogous process, however, it is not possible to simulate the plunge shaving process, since only one cutting edge is used. On the other hand, the FE-based simulation model can also be used for this process in order to determine the loads on the tool with respect to different technological parameters, like the cutting speed, plunge feed rate, axial feed rate, crossed-axis angle and cutting edge roundness.

At first, the cutting speed is varied. In the upper part of Figure 11, the chip creation from a state-of-the-art plunge shaving process is shown at the beginning of the cut and at the point with the highest chip thickness. As in Figure 10, the stress within the workpiece flank is shaded dark, but in this case, the stress in the tool is also shown.

Figure 11--Chip creation with respect to the cutting speed.

The lower part of the figure shows the chip creation at a cutting speed of vc = 120 m/min in the same spots as in the upper part. Even though the cutting speed has been increased by three times, no remarkable change in the chip creation can be observed.

As a next step, the chip creation with respect to cutting edge geometry is shown in Figure 12. It can be seen that also in plunge shaving, there is a clear dependence of the chip creation on the shape of the cutting edge. Unlike the analogous process, the tool wear in real shaving processes is reflected in a higher cutting edge radius rather than as a chamfer on each side of the cutting edge (Ref. 4). Therefore, this cutting edge geometry has not been studied in this case.

Figure 12--Chip creation in plunge shaving with respect to the cutting edge geometry.

The cutting edge used in this simulation had a radius of ? = 20 µm. Again, the chip creation clearly depends on the cutting edge radius. Compared to the chip creation in Figure 11, where a cutting edge radius of ? = 5 µm was simulated, the chip in this case is more deformed and more compact. In the lower right side of the figure, the deformation of the chip is quantified. The ratio of 24 µm to 10 µm from deformed chip thickness to undeformed chip thickness indicates a shortening of factor 2.4.

Also, in the lower left side of that picture, a fold can be seen. During the simulation, these folds occurred several times, which led to problems with the simulation. The mesh size had to be increased in order to allow the simulation to continue. This fold indicates a creation of lamella chips.

It is obvious that the cutting edge geometry also has an impact on the process forces. Thus, in Figure 13, the process forces for the two different cutting edge geometries are shown. In the upper part of the figure, the actual cutting force is displayed, while in the lower part, the passive forces—which are perpendicular to the cut—are shown. It can be seen that during the chip creating period of the cut, the cutting forces are increased by about 60% and the passive forces by more than 100% due to the higher cutting edge radius. This effect can be considered to be the main reason for the quality reduction that results when a gear is machined with this type of cutting edge geometry.

Figure 13--Process forces with respect to the cutting edge geometry.

In the next step, the plunge (or radial) feed rate has been varied. The cutting forces of this study are displayed in Figure 14. Beginning with the state-of-the-art plunge shaving process, where the plunge feed rate is about 2 µm per workpiece revolution, the plunge feed rate has been increased to 3, 4.5 and 6 µm.

Figure 14--Process forces depending on the plunge feed rate.

Again, it is obvious that the increase of the feed rate has a clear effect on the process forces. The maximum cutting force is increased by about 80% and the maximum passive force is increased by about 90%. Another important phenomenon that can be observed in Figure 14 is that one cut can be divided into two parts. Shortly after the first contact between tool and workpiece, both the cutting and passive forces reach their maximum values. The maximum is much higher for the passive forces than for the actual cutting forces, which indicates that the maximum forces are caused by the workpiece material, which has to be plastically deformed underneath the flank of the cutter due to negative clearance angles. After reaching their maximums, both forces drop quickly down to a minimum value when the path of the cutting edge has reached the deepest point in the workpiece flank. At that time, the actual chip creation begins, and the curve follows the chip thickness value along the cut. Thus, it can be stated that the first stage of the cut is the deforming stage, and the second stage is the cutting stage.

The maximum overall load during the cut for all plunge feed rates occurs during the deforming stage. Therefore, the load on the flank of the shaving cutter is higher than that on the rake face, since the flank is already in contact during the deforming stage, while the rake face is only in contact when a chip is formed.

In the last step, the axial feed rate has been varied. In real plunge shaving processes, varying the axial feed rate is only possible by modifying the tool. Therefore, it is very costly to perform trials in real shaving processes with different axial feed rates. In this paper, the axial feed rate has been varied, beginning with an industrial standard of 0.2 mm per workpiece revolution and increasing it to 0.4 mm per workpiece revolution. The process forces for this variation are displayed in Figure 15.

Figure 15--Process forces depending on the axial feed rate.

Again, the cuts can clearly be divided into two phases. The increase of the axial feed rate leads to a significant increase of the deforming phase. On the one hand, the share of the deforming phase along the cut is larger, and on the other hand, the forces during the deforming phase are higher due to the larger amount of material that has to be deformed underneath the clearance face.

During the variation of the feed rates, it was shown that an increase of both types of feed rates causes a strong increase of the passive forces during the deforming phase of the cuts. Therefore, it can be assumed that also the quality of the machined gears will be worse when either one of the two feed rates is increased. In contrast to that, the increase of the cutting speed has not shown significant influence on the cutting process.

Summary and Outlook
It was the aim of the work described in this report to show approaches for an optimization of gear shaving using different simulation techniques. At first, a detailed description of the gear shaving process and its technological peculiarities was given. After this, an analogous process was introduced that can be used for systematic technological wear studies in gear shaving. It was shown that, in the analogous process, similar chip geometries as in real shaving can be created.

In the next step, a simulation model was introduced that is based on penetration calculation. This model was used subsequently to determine the path of the cutting edges during the cutting operation. The results of this simulation were used as input data for another simulation type, based on FEA. This type of simulation allows for a detailed modeling of machining processes considering the process kinematics and geometric boundary conditions as well as the material data. As a result, measures like temperatures, stresses, forces and others can be determined on the surface or inside both the tool and the workpiece (Ref. 2).

Within the scope of this report, among the large number of possible outputs, mainly the process forces and the chip creation have been studied. At first, the simulation was verified using the analogous process introduced before. By simulating different cutting edge geometries, the effect on the chip creation was studied and compared to the results obtained in the analogous process.

In the next step, a commonly used plunge shaving process was simulated. Again, the effect of the cutting edge geometry on the forces and the chip creation was studied. For this, the radius of the cutting edge was increased to a value of ? = 20 µm. This increase corresponds to a radius that, in previous studies, was measured on a shaving wheel that was considered to be worn. Within the simulation, it could be shown that the cutting edge geometry has a strong effect on the chip creation process. The chips are significantly shorter and crushed during the cut. Also, both the cutting and passive forces are on a higher level than with a sharp tool.

The variation of the cutting speed does not show a significant effect on the chip creation but the results show that one cut in plunge shaving can generally be divided into two phases. In the beginning of the cut, there is a negative effective clearance angle leading to material deformation underneath the tool flank. This phenomenon can be seen in a high peak within the progression of the passive force. After this so-called deformation phase, the actual chip creation phase begins. After the deepest point on the track of the cutting edge has been passed, a positive clearance angle exists, and the passive forces decrease significantly.

In contrast to the cutting speed, the chip geometry, which can be modified by the plunge or the axial feed rate, has a strong effect on the process forces. In any case, the increase of each of the named values leads to an increase in the passive forces, while the cutting forces can only be slightly influenced.

As a conclusion it can be stated that the FE-based machining simulation, in combination with the simulation based on penetration calculation, represents a valuable tool in order to analyze and optimize the gear shaving process in detail. The simulation can be used to determine the loads on the cutting edge under the specific boundary conditions of the gear shaving process. In further studies, this simulation will be used to simulate the complete shaving wheel tooth in contact with the workpiece tooth in a three-dimensional simulation. Thereby, the deflection of the teeth under the load of the gear shaving process can be studied, and the reasons for the created gear quality can be found.

Printed with the friendly permission of the publisher from VDI-Gesellschaft Entwicklung, Konstruktion, Vertrieb (Editor): International Conference on Gears, Vol. 1, VDI Report 1904. VDI-Verlag, Düsseldorf, Germany, 2006, pp. 823–841 (first publication). Appeared in VDI Report 1904 under the title “Optimisation of Gear Shaving by Application of Simulation Techniques.”

References

1. Klocke, F., H. Schlattmeier, and T. Schröder. “Optimierung des Schabprozesses zur Erhöhung der Wirtschaftlichkeit und der Prozesssicherheit,” Proceedings of Seminar “Feinbearbeitung von Stirnrädern in der Serie,” Aachen, Germany, Dec. 3–4, 2003.

2. Klocke, F., and T. Schröder. Simulation des Zahnradschabens, wt Werkstattstechnik Online, 6 (2005).

3. Becker, J. “Weichschaben, die wirtschaftliche Zahnflankenbearbeitung–Heutiger Stand und Entwicklungstendenzen,” Proceedings of TAE-Seminar “Praxis der Zahnradfertigung,” Esslingen, Germany, June 28–30, 2000.

4. Klocke, F., and T. Schröder. “Gear Shaving–Simulation and Technological Studies,” Proceedings of DETC ’03, ASME 2003 Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, Sept. 2–6, 2003.

5. Klocke, F., H.W. Raedt, S. Hoppe, G. Messner, and L. Markworth. “Application of the EF-Method to the Machining Process,” CIRP Modeling Workshop, Paris, France, 2002.

Prof. Dr.-Ing. Dr.-Ing. E.h. Fritz Klocke is head of the Chair of Manufacturing Technology at the Laboratory for Machine Tools and Production Engineering (WZL), a part of Aachen University of Technology in Germany. Also, he is director of the Fraunhofer Institute for Production Technology in Aachen, Germany.

Dipl.-Ing. Tobias Schröder is chief engineer of WZL’s gear department, where he supervises current projects and proposes future ones. Schröder has conducted several research projects in gear shaving. Also, he completed his doctoral dissertation on gear shaving and is awaiting its publication.