Carlo Innocenti

(This article first appeared in the proceedings of IMECE2007, the 2007 ASME International Mechanical Engineering Congress and Exposition, November 11–15, 2007, Seattle, Washington, USA. It is reprinted here with permission.)

Management Summary
It is the intent of this presentation to determine all rigid-body positions of two conical involutes that mesh together, with no backlash. That information then serves to provide a simple, general approach in arriving at two key setting parameters for a hobbing machine when cutting a conical (beveloid) gear. A numerical example will show application of the presented results in a case study scenario. Conical involute gears are commonly seen in gearboxes for medium-size marine applications—onboard engines with horizontal crankshafts and slightly sloped propeller axes—and in automatic packaging applications to connect shafts with concurrent axes whenever the angle between these axes is very small (a few degrees).

Introduction
Conical involute gears, also known as beveloid gears, are generalized involute gears that have the two flanks of the same tooth characterized by different base cylinder radii and different base helix angles (Refs. 1– 4). Beveloid gears can be mounted on parallel-, intersecting- or skew-axis shafts. They can be cheaply manufactured by resorting to the same cutting machines and tools employed to generate conventional, involute helical gears. The only critical aspect of a beveloid gear pair, i.e., the theoretical punctiform (single-point) contact between the flanks of meshing gears, can be offset by a careful choice of the geometric parameters of a gear pair (Refs. 5–7). On the other hand, the localized contact between beveloid gear teeth comes in handy should the shaft axes be subject to a moderate, relative position change in assembly or operation.

The technical literature contains plenty of information regarding the tooth flank geometry (Refs. 8–9) and the setting of a hobbing machine in order to generate a beveloid gear (Refs. 10–15). Unfortunately, the formalism usually adopted makes determination of the hobbing parameters a rather involved process, mainly because the geometry of a beveloid gear is customarily—though inefficiently—specified by resorting to the relative placement of the gear with respect to the standard rack cutter that would generate the gear, even if the gear is to be generated by a different cutting tool. To make things worse, some of the cited papers on beveloid gear hobbing are hard reading due to printing errors in formulae and figures.

This paper presents an original method to compute the parameters that define the relative movement of a hob with respect to the beveloid gear being generated. Pivotal to the proposed method, together with a straightforward description of a beveloid gear in terms of its basic geometric features, is the determination of the set or relative rigid-body positions of two tightly meshing beveloid gears. Based on this set of relative positions, the paper shows how to assess the rate of change of the hob-work shaft axis distance as the hob is fed across the work, as well as the rate of the additional rotation of the hob relative to the gear. These parameters have to be entered into the controller of a CNC hobbing machine in order to generate a given beveloid gear.

The proposed method also can be applied to the grinding of beveloid gears by the continuous generating grinding process. Furthermore, it can be extended to encompass the cases of swivel angle modification and hob shifting during hobbing.

Lines of Contact
The hob that generates a beveloid gear in a hobbing machining process can be considered an involute gear. Most commonly, such a gear is of the cylindrical type, although adoption of a conical involute hob would be possible too, in principle. For this reason, the kinematics of hobbing will be presented in this paper by referring to a beveloid hob, and subsequently specialized to the case of a cylindrical hob.

This section introduces the nomenclature adopted in the paper and summarizes known results pertaining to the loci of contact of a conical involute gear set. The reader is referred to References 16 and 17 for a detailed explanation of the reported concepts and formulas.

The tooth flanks of a conical involute gear are portions of involute helicoids. As opposed to classical helical involute gears, the two helicoids of the same tooth of a conical involute gear do not generally stem from the same base cylinder, nor have the same lead.

In a beveloid gear set composed of gears G1 and G2, the axis of gear G1 is here directed in either way by unit vector n1. The orientation of the axis of gear G2 by unit vector n2 is then so chosen as to make the right-hand flanks of gear G1 come into contact with the right-hand flanks of gear G2.

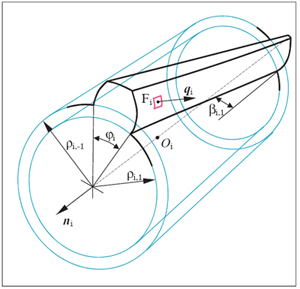
Figure 1—Basic dimensions of beveloid gear Gi.

With reference to Figure 1, the distinction between right-hand and left-hand tooth flanks is possible based on the sign of the ensuing quantity:

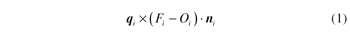
where Fi is a point on a tooth flank of gear Gi (i=1, 2), Oi is a point on the axis of gear Gi, and qi is the outward-pointing unit vector perpendicular to the tooth flank at Fi. A tooth flank is a right-hand or left-hand flank, depending on whether Equation 1 results in a positive or, respectively, negative quantity. (In Figure 1, point Fi lies on a right-hand flank of gear Gi). In the sequel, index j will be systematically used to refer to right-hand (j = + 1) or left-hand (j = −1) tooth flanks.

The basic geometry of gear Gi (i=1, 2) is defined by its number of teeth Ni, the radii ρi,j (j = ± 1) of its base cylinders, the base helix angles βi,j of its involute helicoids (βi,j< π/2; βi,j > 0 for right-handed helicoids), and the base angular thickness φ'i of its teeth at a specified cross section. All these parameters—with the exception of Ni—are reported in Figure 1, which also shows the involute helicoids as stretching inwards up to their base cylinders, irrespective of their actual radial extent.

The normal base pitch is the distance between homologous involute helicoids of adjacent teeth of the same gear. A beveloid gear has two normal base pitches—pi,1 and pi,–1—one for right-hand flanks and one for left-hand flanks. Their expression is:

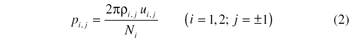
where

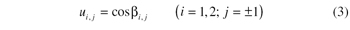
Two beveloid gears can mesh only if they have the same normal base pitches, i.e., only if the ensuing conditions are satisfied:

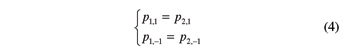
Owing to Equation 4, the following equations and ensuing text and figures will refer to the normal base pitch of right-hand and left-hand flanks of both gears as p1 and p–1 respectively.

The common perpendicular to the axes of a pair of meshing beveloid gears intersects the axes themselves at points A1 and A2 (Fig. 2). The relative position of these axes is defined by their mutual distance a0, together with their relative inclination α0. Specifically, angle α0 is the amplitude of the virtual rotation—positive if counterclockwise—about vector (A2–A1) that would make unit vector n1 align with unit vector n2. Two fixed Cartesian reference frames Wi (i =1, 2) are then introduced with origins at points Ai, xi axis pointing towards A3– i, and zi axis directed as unit vector ni.

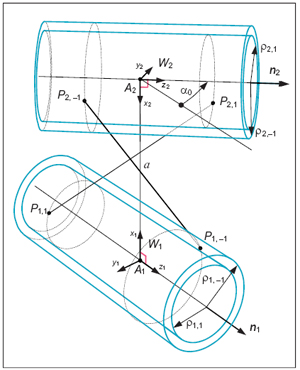
Figure 2—The lines of contact.

For a conventional beveloid gear set composed of two meshing conical involute gears that revolve about their fixed and non-parallel axes, the locus of possible points of contact between the involute helicoids of right-hand (left-hand) flanks is a line segment that has a definite position with respect to either of reference frames Wi (i=1, 2). More specifically, the line of contact is tangent at its ending points P1,1 and P2,1 (P1,–1 and P2,–1) to the base cylinders of the right-hand (left-hand) flanks of the two gears. This is true even if the actual tooth flanks—being limited portions of the above-mentioned involute helicoids—touch each other along line segments that are shorter than the above-mentioned lines of contact and superimposed on them.

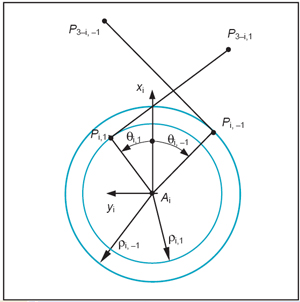
Figure 3—Coordinates of the extremities of the lines of contact.

The cosine and sine of the angle θi,j that the projection of vector (Pi,j –Ai) on the xy-plane of reference frame Wi forms with the x-axis of Wi (see Fig. 3) are indirectly provided by:

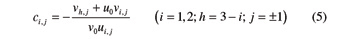
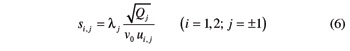
where

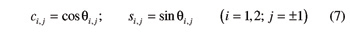
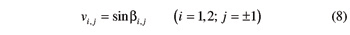
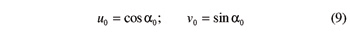
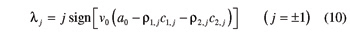
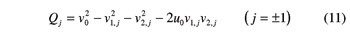
The function sign(.) in Equation 10 returns the value + 1, 0, or –1 depending on whether its argument is positive, zero or negative. In Figure 3, angle θi,1 is positive, whereas angle θi,–1 is negative.

Due to the square root in Equation 6, two beveloid gears can properly mesh only if condition

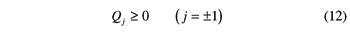
is satisfied for both values of j. In the following equations, text and figures Equation 12 will be supposed as holding.

Thanks to Equations 5 and 6, angle θi,j can be expressed as:

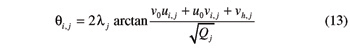
(i=1,2; h= 3 – i; j= ± 1).

The z-coordinate bi,j of point Pi,j in reference frame Wi (i=1,2; j= ± 1) is given by:

b1,j=

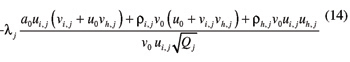
Based on the relative positions of reference frames W1 and W2, together with the cylindrical coordinates ρi,j, θi,j, and bi,j of points Pi,j with respect to Wi (i=1,2; j= ± 1), the length σj of the line of contact P1,jP2,j can be determined by (Refs. 16–17):

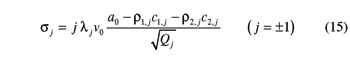
The results summarized so far are directly applicable to a conventional beveloid gear set, i.e., to a pair of meshing beveloid gears that revolve about their rigidly connected axes. They also represent a convenient starting point for determining all possible relative positions of a beveloid hob relative to the beveloid gear being machined.

A Backlash-Free Beveloid Gear Set
Due to the single-point contact between tooth flanks of a beveloid gear set, the assortment of rigid-body positions of a beveloid hob relative to the beveloid gear being machined cannot be confined to the simple infinity of relative positions of two gears in a conventional beveloid gear set. Otherwise, a gear machined by a beveloid hob would not have involute helicoidal flanks; rather, only one curve on these flanks would belong to the desired involute helicoids.

Therefore the double infinity of points on a tooth flank of a beveloid gear machined by a beveloid hob has to be obtained at least as a two-parameter envelope of the positions of the hob tooth flanks. Each of these positions must correspond to a meshing configuration—with no backlash—of the beveloid hob with the finished beveloid gear.

There is a quadruple infinity of configurations of a beveloid gear tightly meshing with a beveloid hob (the contacts between right-hand flanks, as well as the contacts between left-hand flanks, each diminish by one the original six degrees of free-dom that possess, in principle, a freely-movable hob that does not touch the gear). The double infinity of rigid-body positions of the hob relative to the generated gear is only a subset of the quadruple-infinity possible meshing configurations. This latter set of configurations can be found by first determining the simple infinity of all relative rigid-body positions of two beveloid gears tightly meshing in a conventional gear set, which is just the scope of the present section.

With regards to the same set of beveloid gears considered in the previous section, let φ0i be the common-normal angular base thickness of a tooth of gear Gi (i=1, 2), i.e., the angular base thickness at the cross-section of gear Gi through point Ai (Figs. 1 and 2). On a generic cross-section identified by the axial coordinate zi, the tooth angular base thickness φi′ of a tooth of gear Gi is given by

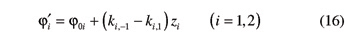
In this equation, quantity ki,j is defined as

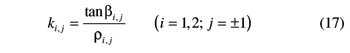
Incidentally, ki,j can be given a geometric meaning: If the base helix of an involute helicoid j of gear Gi is projected on the unitary-radius cylinder coaxial with the gear, then the resulting projection is a helix whose inclination angle with respect to the gear axis is tan–1ki,j.

If the surface of the unitary-radius cylinder of gear Gi is now cut along the generator that intersects the negative x-axis of reference frame Wi (Fig. 2), and subsequently flattened (Fig. 4), the former projections of the base helices of a tooth of gear Gi appear as straight lines. In Figure 4, coordinate δi—measured from the generator that intersects the positive x-axis of Wi—parameterizes the generators of the unitary-radius cylinder associated with gear Gi. The common-normal angular base tooth thickness φ0i is also shown in Figure 4, together with the point Hi of intersection of the common normal A1A2 with the unitary-radius cylinder of gear Gi.

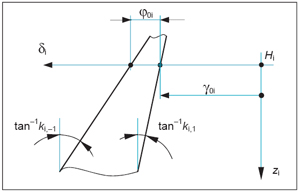
Figure 4—The developed unitary-radius cylinder of gear Gi.

The orientations of gears G1 and G2 about their respective axes are defined here by considering an arbitrarily selected reference right-hand flank (involute helicoid) Σ1,1 on gear G1, together with the right-hand flank (involute helicoid) Σ2,1 of the tooth of gear G2 in contact with Σ1,1. The reference angular position of gear Gi is chosen here as characterized by helicoid Σi,1 intersecting the minimum distance segment A1A2 (Fig. 2) at a point of the base cylinder of gear Gi (i=1,2). (Equivalently, at the reference angular position of gear Gi the projection of the base helix of Σi,1 on the unitary-radius cylinder of the gear goes through point Hi.) A generic angular position of gear Gi is then identified by the angle γ0i of the rotation that carries the gear from its reference angular position to the considered position. Angle γ0i—positive for a counterclockwise rotation with respect to unit vector ni (Fig. 2), can also be highlighted on the developed unitary-radius cylinder (Fig. 4).

The angular positions γ01 and γ02 of two beveloid gears that mesh together with zero backlash are clearly interrelated. An obvious mutual constraint is the differential condition that stems from expressing the gear ratio in terms of the number of teeth Ni (i=1,2) of the two gears

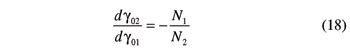
In order to find a finite relation between γ01 and γ02, two maneuvers are envisaged. The first maneuver starts with the first gear at position γ01= 0 and—by exploiting the tooth contact between right-hand flanks only—carries the second gear at position γ02= 0. The second maneuver is similar to the first one, but for the reliance on the contact between left-hand flanks.

The first step of the first maneuver consists of making the reference involute helicoid Σ1,1 of gear G1 go through the extremity P1,1 of the line of contact between helicoids of right-hand flanks (Fig. 2). The corresponding rotation Δγ01a of gear G1 is given by

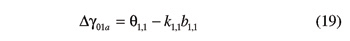
where θ1,1 and b1,1 are provided by Equations 13 and 14, respectively. Equation 19 can be justified by elementary geometric reasoning on the unitary-radius cylinder of gear G1. (The reader is referred to Reference 16 for further details.)

The second step makes helicoid Σ1,1 go through point P2,1. The necessary rotation of gear G1 is

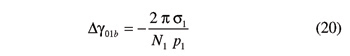
Now helicoids Σ1,1 and Σ2,1 touch each other at P2,1. By the third—and last—step, gear G2 is so turned about its axis as to make the base helix of helicoid Σ2,1 intersect the common normal A1A2. The corresponding rotation of gear G2 is given by

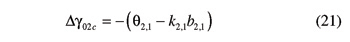
At the end of the considered three-step maneuver, gear G2 is at its reference position (γ02 = 0), whereas gear G1 is at a position identified by

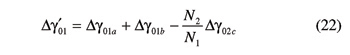
Owing to Equation 18, and to the existence of a meshing configuration characterized by (γ01, γ02 ) = (Δγ′01, 0) , the ensuing relation between γ01 and γ02 must be satisfied

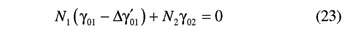
Now the second maneuver is taken into account. Its first step consists of bringing gear G1 from the reference angular position to the position where helicoid Σ1,–1 goes through point P1,–1. Here Σ1,–1 is the helicoid that, together with the reference helicoid Σ1,1 defined above, bounds the same tooth of gear G1. The corresponding rotation of gear G1 is (see Figs. 2–4):

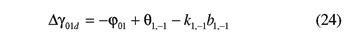
By the second step, gear G1 is revolved until helicoid Σ1,–1 goes through point P2,–1. The incremental rotation of gear G1 is provided by

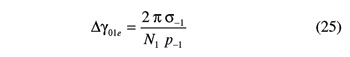
After this step, the helicoid Σ1,–1 of gear G1 touches the helicoid Σ2,–1 of gear G2 at point P2,–1. It is worth observing that, while Σ1,1 and Σ1,–1 bound the same tooth of gear G1, Σ2,1 and Σ2,–1 delimit the same tooth space of gear G2.

The third step of the current maneuver consists in making helicoid Σ2,–1 intersect the common normal A1 A2 at a point of its base helix. The additional rotation of gear G2 is provided by

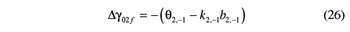
The fourth—and last—step brings gear G2 at the reference position γ02 = 0, i.e., makes helicoid Σ2,1 intersect the common normal A1A2 at a point of the base helix. The corresponding further rotation of gear G2 is

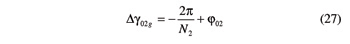
The angular position of gear G1 at the end of the whole maneuver is provided by

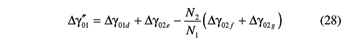
Therefore in addition to Equation 23, another constraint between γ01 and γ02 can be found

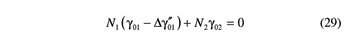
By considering the expressions of Δγ'01and Δγ"01 provided by Equations 22 and 28, Equations 23 and 29 can be rewritten as

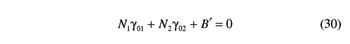
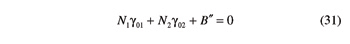
Quantities B' and B" that appear in these equations are given by

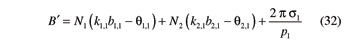
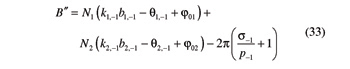
For a given backlash-free beveloid gear set, Equations 30 and 31 must be satisfied simultaneously. Since the considered gear set is a mechanism with one degree of freedom, it should be possible to arbitrarily select γ01 (or γ02), and then determine γ02 (or γ01). Therefore Equations 30 and 31, when considered as linear equations in γ01 and γ02, should be linearly dependent. This requirement translates into the ensuing condition:

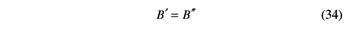
By taking into account Equations 32 and 33, Equation 34 can be rewritten as follows (Ref. 16):

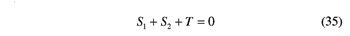
where

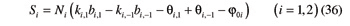
and

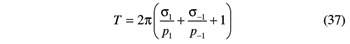
Equivalent to the equation set composed of Equations 30 and 31, the equation set formed by Equations 30 and 35 encapsulates the meshing condition—with no backlash—of a pair of conical involute gears, each bound to revolve about its own axis. More specifically, Equation 35 involves the geometry of the two beveloid gears, together with the relative placement of the two gear axes and the axial placement of each gear on its own axis. It had already been presented, though in a slightly different form, in Reference 16. On the other hand, by also encompassing the angular position of the two gears, Equation 30 provides information about their phasing. To this author’s knowledge, no such equation has ever been published before.

Unconstrained Beveloid Gears in Tight Mesh
As anticipated at the beginning of the previous section, the whole collection of relative rigid-body positions of two tightly meshing beveloid gears can be determined by generalizing the results just found for a conventional beveloid gear set.

Let us consider again a beveloid gear set, composed of two meshing beveloid gears connected to a rigid frame through revolute pairs. If the distance a0 and angle α0 between the revolute pair axes, together with the geometry of the two gears—notably their common-normal base angular thicknesses φ01 and φ02—comply with Equation 35, then Equation 30 is satisfied by a simple infinity of values for the ordered pair (γ01, γ02), i.e., the mechanism has a simple infinity of configurations.

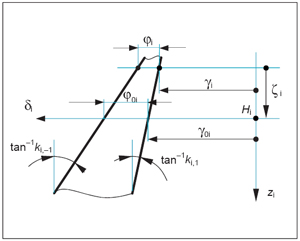
Figure 5—Reference and common-normal parameters.

Now the two mentioned revolute pairs are replaced by cylindrical pairs, which implies that both gears can be displaced along their axes, in addition to being revolved about them. Consequently, the common-normal base angular thickness φ0i of gear Gi, i.e., the base angular thickness on a cross section of gear Gi going through point Ai (Fig. 2), becomes linearly dependent on the axial placement of the gear. With the aid of Figure 5, the ensuing condition can be laid down (See also Eq. 16)

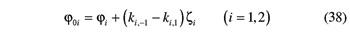
In this equation, φi is the reference base angular thickness of gear Gi, i.e., the base angular thickness of a tooth of gear Gi at a reference cross section fixed to the gear. Moreover, ζi is the displacement of the common-normal cross section, measured from the reference cross section, positive if concordant with the direction of the z-axis of reference frame Wi (a positive ζi is shown in Figure 5).

Quantity γ0i is no longer suited to parameterize the angular position of gear Gi. For instance, if γ0i = 0 and gear Gi is axially displaced, then the base helix of the reference helicoid Σi,1 keeps intersecting the minimum distance segment A1A2, which means that the gear undergoes a screw motion with respect to the rigid gear-set frame, thus changing its orientation.

Henceforth the angular position of gear Gi will be parameterized by angle γi, which is an angle measured on the reference cross section of the gear. Precisely, γi is the angle between two lines belonging to the reference cross section of gear Gi—the projection of the minimum distance segment A1A2, and the radial line through the point on the base helix of reference flank Σi,1. As shown in Figure 5, the following relation exists between γ0i and γi

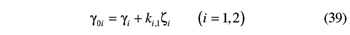
By taking into account Equations 38 and 39, Equations 35 and 30 are transformed into a set of two equations in the four unknowns ζ1, ζ2, γ1 and γ2. It is generally possible to arbitrarily choose either of γi (i=1,2) and either of ζi (i=1,2), and then determine the remaining two unknowns. Therefore a set of two beveloid gears connected to the frame by cylindrical pairs has two degrees of freedom, with no need to satisfy any prerequisite similar to Equation 35.

At this point, the frame of the gear set is suppressed altogether, so that parameters a0 and α0 are no longer bound to be constant. We are now left with two beveloid gears that can be freely moved in space, provided that they keep meshing with no backlash. All relative rigid-body positions of the two gears are those satisfying Equations 35 and 30, which can be rewritten in the ensuing concise form

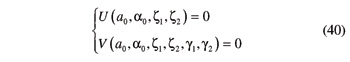
In Equation 40, U and V are, respectively, what the left-hand sides of Equations 35 and 30 turn into, once φ0i and γ0i (i=1,2) have been replaced with the expressions provided by Equations 38 and 39.

Equation 40 is a set of two conditions in six unknowns, namely, a0, α0, ζ1, ζ2, γ1 and γ2. Therefore, Equation 40 can be solved in a quadruple infinity of ways, which means that there is a quadruple infinity of possible relative placements for the two beveloid gears.

As explained hereafter, each of these relative placements can be determined by relying on the values of a0, α0, ζ1, ζ2, γ1 and γ2. At first, a skeleton is built based on a0 and α0. Such a skeleton is formed by the axes of the two gears, together with the common normal segment A1A2 (Fig. 2). Subsequently gear Gi (i= 1,2) is axially placed on its axis by relying on the value of ζ1. Finally, the orientation of gear Gi about its axis—and with respect to the skeleton segment A1A2—is provided by angle γi.

Equation 40 will prove pivotal in computing the hobbing parameters of a beveloid gear.

Gear-Hob Relative Movements
As already mentioned at the beginning of the section addressing a backlash-free beveloid gear set, the tooth flanks of a beveloid gear result from a two-parameter envelope by the hob thread flanks. The double-infinite subset of the quadruple infinity of possible gear-hob relative placements is chosen here on the analogy of the hobbing operation of a cylindrical gear by a cylindrical hob. Throughout this section, the generated gear and the enveloping hob will be referred to as gear G1 and G2 respectively.

As is known, a cylindrical gear can be hobbed by keeping constant the work-hob axis angle α0, by revolving the hob about its axis, and by simultaneously moving such an axis across the gear width. In case no hob shift takes place during hobbing—as usually happens—parameter ζ2 is kept constant too. If the gear and the hob are both cylindrical, it is easy to prove that function U in Equation 40 is deprived of arguments ζ1 and ζ2. Therefore, the constancy of the shaft angle α0 implies the constancy of the axis distance a0, too; parameters γ1 and ζ1 can be thought of as the two parameters of the enveloping process. And for any choice of their values, the second condition in Equation 40 yields quantity γ2.

Now the hobbing of a beveloid gear by a beveloid hob is analyzed. Similar to the previous case, the shaft angle α0 is supposed as constant. Its value might be chosen, for instance, with the aim of minimizing the shaft axis distance a0 at a given cross-section of the gear (see, for instance, Reference 17 for application of this criterion to the hobbing of cylindrical gears). The independent parameters of the envelope are again γ1 and ζ1, whereas parameter ζ2 is kept constant. For any choice of γ1 and ζ1, the first and second conditions in Equation 40 yield, respectively, the values of a0 and γ2.

The instantaneous movement of the hob relative to the gear being machined can be thought of as the superimposition of two movements:

1. The relative movement of hob and gear as they revolve about their axes (only the independent envelope parameter γ1 varies)

2. The relative movement of hob and gear when the gear is shifted along its axis without turning with respect to the hobbing machine (only the independent envelope parameter ζ1 varies)

Since the former movement can be found straightforwardly via Equation 18, only determination of the latter will be pursued here. More specifically, the ensuing ratios of differentials are of interest

The differentials on the right-hand sides of Equation 41 are computed with these assumptions

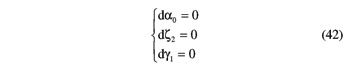
Ratio ƒa is the rate of change of the gear-hob axis distance as the hob is moved along the gear width; it is zero for cylindrical gears, but not so for beveloid gears. Ratio ƒγ, on the other hand, provides information about the hob rotation as the hob is fed across the work. It would be zero for a spur gear, but is different from zero for helical gears and for most beveloid gears.

To compute ratios ƒa and ƒγ, Equation 40 is now differentiated by taking into account Equation 42

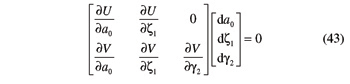
Based on Equation 43, the ensuing expression for quantities ƒa and ƒγ can be obtained

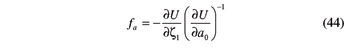
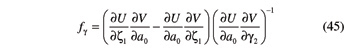
The partial derivatives in Equations 44 and 45 can be easily computed as shown hereafter. The partial derivative of U with respect to a0 is given by the ensuing concatenation of relations

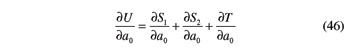
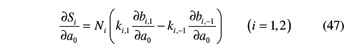
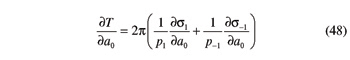
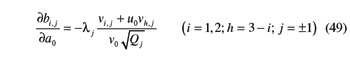
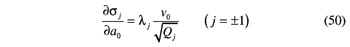
As for the partial derivative of U with respect to ζ1, it is provided by

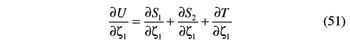
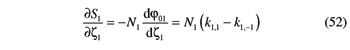
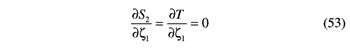
The partial derivative of V with respect to a0 is given by

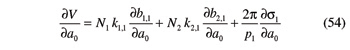
The derivatives on the right-hand side of this equation are in turn provided by Equations 49 and 50.

Finally, the partial derivative of V with respect to ζ1 and γ2 can be easily determined based on Equations 30 and 39:

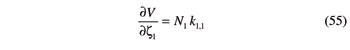
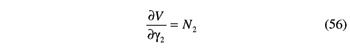
Thanks to Equations 46–55, the ratios fa and fγ can be re­written in the ensuing explicit form:

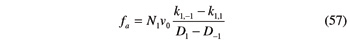
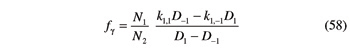
Quantities Dj (j= ± 1) in Equations 57 and 58 are defined by:

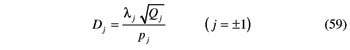
Equations 57–59 show that ƒa and ƒγ, do not depend on ζ1, but only on the geometry of gear and hob, together with the swivel angle α0 (which has been supposed as constant). The constancy of ƒa, in particular, explains why the root surface of a beveloid gear is conical—at least if the gear is cut by keeping constant the angle α0.

Equation 59 provides the expression of Dj (j= ± 1) for any pair of beveloid gears. When gear G2 is a hob, the number of teeth N2 is small and the absolute values of the base helix angles β2,1 and β2,−1 are relatively large. Therefore the ensuing inequality is generally satisfied

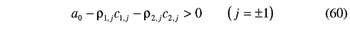
Consequently, Equation 10 reduces to

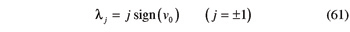
In addition, since the most commonly used hobs can be considered as involute cylindrical gears rather than beveloid gears, the ensuing additional conditions come into play

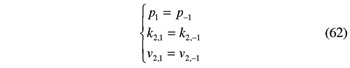
The values of ratios ƒa and ƒγ, are always needed when programming a CNC hobbing machine that has to cut a beveloid gear. Thanks to Equations 57 and 58, these ratios can be straightforwardly assessed. Therefore, from a utilitarian standpoint, Equations 57 and 58 are the main result of this paper.

Should angle α0 change while ζ1 varies (for instance, to constantly minimize the shaft distance a0), and/or hob shifting occur during machining (for instance, to reduce the scalloping of the tooth flanks of the gear), then the mentioned equations would no longer be applicable. In this occurrence, Equation 40—the true theoretical contribution of this paper—should be resorted to again, and applied afresh to the case at hand.

Numerical Example
The formulae derived in the previous section are here applied to determine quantities ƒa and ƒγ for the hobbing of a beveloid gear (gear G1) by a cylindrical hob (gear G2).

Throughout this section, non-integer quantities are expressed by a high number of digits—all meaningful—in order to allow the reader to accurately check the reported result.

The hob has one thread (N2 = 1) and is characterized by a module of 2 mm and a pressure angle of 20°. Based on this data, the ensuing dimensions can be easily computed

ρ2,1= ρ2,–1= 2.735229431127 mm

β2,1= β2,–1= 69.90659103379 deg

φ2 = 1220.353746100 deg

The normal base pitches of hob and gear can be derived from the geometry of the hob

p1= p-1= 5.904262868187 mm

The gear is characterized by

N1=14

ρ1,1 = 13.16838183156 mm

ρ1,-1 = 13.15931278723 mm

β1,1 = –2.515092347823 deg

β1,-1 = –1.343231785965 deg

On a given (reference) cross section of the gear, the angular base thickness of the gear teeth is:

φ1= 16.94800000000 deg

The angle α0 between the axes of gear and hob is chosen in such a way as to minimize the shaft distance a0 when point A1 (Fig. 2) lies on the mentioned reference cross section of the gear. The corresponding values of α0 and a0 are:

α0 = –86.03648170877 deg

a0 = 43.96806431329 mm

The ratio fa between the change of axis distance a0 and the displacement ζ1 of point A1 (Figs. 2 and 5) along the gear axis is provided by Equation 57

ƒa = 0.02988732132842 mm/mm

On the other hand, the ratio ƒγ between the rotation angle of the hob and the displacement ζ1 of point A1 along the gear axis—when the gear does not rotate with respect to the hobbing machine—is provided by Equation 58

ƒγ = 2.050765894724 deg/mm

(To obtain this value, a conversion of unit of measurement has been necessary, since the ratio ƒγ yielded by Equation 58 is expressed in radians per unit of length.)

Conclusions
With reference to the generation of a beveloid gear by a hobbing machine, the paper has presented a simple and general method to determine the rate of change of the hob-work axis distance and the differential rotation of the hob as the hob itself is fed across the work. Because it relies on a very few intrinsic dimensions of a beveloid gear, the method is conducive to concise expressions for the desired quantities.

The results presented here refer primarily to the hobbing of a beveloid gear by a beveloid hob, provided that the swivel angle remains constant. On the one hand, they can be readily specialized to the case of a cylindrical hob cutting a beveloid gear. On the other hand, it is easy to extend them to make provision for hob shifting and swivel angle change during hobbing.

References
1. Merritt, H.E. Gears, 1954, 3rd Edition, Sir Isaac Pitman & Sons, London.

2. Beam, A.S. “Beveloid Gearing,” 1954, Machine Design, 26, pp. 36-49.

3. Smith, L.J. “The Involute Helicoid and the Universal Gear,” Gear Technology, Nov/Dec., 1990, pp. 18–27.

4. Townsend, D.P. Dudley’s Gear Handbook, 1991, McGraw-Hill.

5. Mitome, K. “Conical Involute Gear (Part 3—Tooth Action of a Pair of Gears),” Bulletin of the JSME, 28, No. 245, pp. 2757–2764.

6. Liu C.-C. and C.-B. Tsay. “Contact Characteristics of Beveloid Gears,” 2002, Mechanism and Machine Theory, 37, pp. 333–350.

7. Börner, J., K. Humm and F.J. Joachim. “Development of Conical Involute Gears (Beveloids) for Vehicle Transmissions,” Gear Technology, Nov./Dec., 2005, pp. 28–35.

8. Liu C.-C. and C.-B. Tsay. “Tooth Undercutting of Beveloid Gears,” 2001, ASME Journal of Mechanical Design, 123, pp. 569–576.

9. Brauer, J. “Analytical Geometry of Straight Conical Involute Gears,” 2002, Mechanism and Machine Theory, 37, pp. 127–141.

10. Mitome, K. “Conical Involute Gear—Analysis, Design, Production and Applications,” 1981, Int. Symposium on Gearing & Power Transmissions, Tokyo, pp. 69–74.

11. Mitome, K. “Table Sliding Taper Hobbing of Conical Gear Using Cylindrical Hob. Part 1—Theoretical Analysis of Table Sliding Taper Hobbing,” 1981, ASME Journal of Engineering for Industry, 103, pp. 446–451.

12. Mitome, K. “Table Sliding Taper Hobbing of Conical Gear Using Cylindrical Hob. Part 2—Hobbing of Conical Involute Gear,” 1981, ASME Journal of Engineering for Industry, 103, pp. 452-455.

13. Mitome, K. “Conical Involute Gear (Part 1—Design and Production System),” 1983, Bulletin of the JSME, 26, No. 212, pp. 299–305.

14. Mitome, K. “Inclining Work-Arbor Taper Hobbing of Conical Gear Using Cylindrical Hob,” 1986, ASME Journal of Mechanisms, Transmissions, and Automation in Design, 108, pp. 135–141.

15. Mitome, K. “A New Type of Master Gears of Hard Gear Finisher Using Conical Involute Gear,” 1991, Proc. of the Eight World Congress on the Theory of Machines and Mechanisms, Prague, Aug. 26–31, pp. 597–600.

16. Innocenti, C. “Analysis of Meshing of Beveloid Gears,” 1997, Mechanism and Machine Theory, 32, pp. 363–373.

17. Innocenti, C. “Optimal Choice of the Shaft Angle for Involute Gear Hobbing,” 2008, ASME Journal of Mechanical Design, 130, pp. 044502.1-044502.5.

Carlo Innocenti is a professor of Mechanics of Machines at the University of Modena and Reggio Emilia, Italy. After obtaining a degree in mechanical engineering in 1984, he worked for two different companies—as a computation engineer and as a mechanical designer, respectively. He then joined academia in 1990. The papers that he has authored or co-authored are mainly focused on the kinematic analysis and synthesis of planar and spatial mechanisms; rotordynamics; vehicle dynamics; robot calibration; gears and gearing systems.