Dr.-Ing. Gottfried Hoffmann and William Jandeska, PhD.

Management Summary
Reducing weight, increasing fuel efficiency, and reducing costs are the most important forces driving the dessire to increase power density of highly loaded transmissions for automobiles, helicopters and other applications. The major failure modes of gears are surface damage due to rolling contact fatigue (RCF), and tooth root bending fatigue.

Despite many years of testing of coupons and gears, the mechanism of surface damage by RCF is still not fully understood. Systematic studies of the material/process parameters on RCF strength are costly and time consuming. That is most often a barrier difficult to overcome.

This article summarizes results of research programs on RCF strength of wrought steels commonly used for gear applications and PM steels, including surface-densified PM preforms. Using eddy current technology in connection with a special RCF test rig allows—for the first time—an in situ study of crack initiation and growth before the actual pitting occurs. This technology will not only lead to a better understanding of failure mechanisms and material behavior, but can also be used to perform systematic tests with a drastically reduced number of test specimens, as well as significantly reduced test time and cost. Hopefully, the application of this procedure will eventually result in material/process RCF-strength relationships that optimize and/or maximize the load carrying capacity of gears and increase transmission efficiency.

Introduction
This is Part I of a two-part article. Part II will be published in the March/April 2007 issue of Gear Techology and presents the results of test programs on the RCF strength of PM steels and discusses the effects on individual material/process parameters on RCF strength.

The desire to improve gear loading capacity is driven by the automotive industry in order to stay competitive in the global market and environment. Therefore, the gear manufacturing industry is encouraged to develop new, cost-effective manufacturing processes that match or improve current gear life without compromising product reliability. However, before advanced materials and/or manufacturing processes are introduced into industrial practice, capabilities and risks must be well-documented in order to:

1. Supply the end-user with reliable property data, comparable to well-known and well-documented traditional materials and/or manufacturing processes.

2. Determine the effects of material and/or process parameters on important design criteria, such as strength under operational conditions, for long-term quality assurance.

3. Support research and development for further improvements or for special applications.

In most cases, these requirements lead to specific product bench testing that provides the confidence and performance data, but often does not translate well to vastly different applications.

This paper summarizes the results of research and development programs on RCF strength of materials for automotive transmission gears. The actual gear contact is very complex and cannot be simulated exactly in any laboratory test equipment (Ref. 1). Therefore, model testing under specific and well-defined test conditions becomes more important because it allows for separating the effects of contact parameters, and for determining the effects of material/process parameters under those specific conditions.

Compared with actual gear testing, model testing reduces test time and costs drastically, but is still too time consuming to study the effect of material/process parameters systematically. Using the eddy current technology to detect failure of the test specimen in very early stages provides additional information about failure mechanisms and crack growth under RCF conditions. Based upon the results of a systematic research program, a procedure was developed that can be used to reduce the number of test samples and allow studying the relative effect of material/process parameters in a very short period of time (Refs. 2–4). The procedure uses the additional information gained by the eddy current technology and can determine changes in RCF strength due to variations of a single parameter.

After describing the most important failure modes under RCF conditions and summarizing the requirements from the designer’s point of view, the paper will introduce the ZF-RCF test rig and the eddy current technology used in connection with the test rig. It will also present test results obtained with wrought steel and PM steels, and will introduce the newly developed procedure for future test programs.

Characterizing RCF Failure
The three-dimensional sub-surface stress field. In order to understand the failure of material under RCF conditions, it is important to understand the complex three-dimensional stress field caused by elastic deformation of the contact zone. The stress field (in terms of maximum contact pressure) is calculated in real arithmetic using a software package (Refs. 5, 6). Figure 1 shows as an example the three dimensional stress field under line contact in the x-direction (σxx is shown in Fig. 1a) and the shear stress (τxy is shown in Fig. 1b) calculated in the contact zone of the ZF-RCF test rig using the following parameters:

1. Contact pressure = 1,800 MPa

2. Radius of test specimen = 15 mm

3. Radius of load roll = 35 mm

4. Young’s moduli = 206 GPa

5. Poisson’s ratio = 0.3

6. Coefficient of friction f = 0

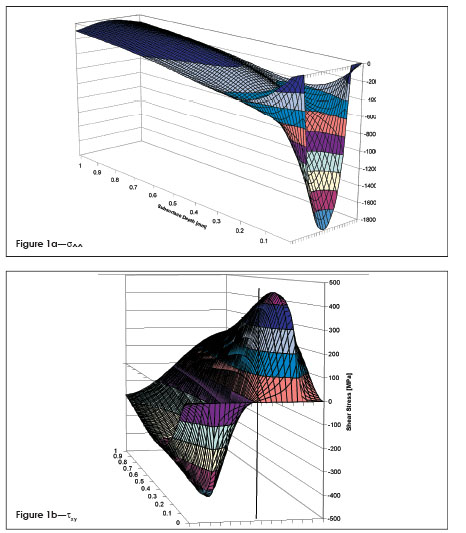
Figure 1—Subsurface stress field due to Hertzian contact pressure.

The contact force produces a complex three-axial stress field within the material (σyy and σzz show similar sub-surface stress distributions as σxx). Only at the line of contact at which τxy = 0 are the stress components identical to the principal stresses σ1, σ2, σ3. Otherwise, magnitude and direction of the principal stresses change at every point. It must be emphasized that all components of the stress tensor are negative (compressive), with the exception of the shear stress, τxy, which is positive before the line of contact and negative thereafter.

From the viewpoint of fatigue, there are several ways to convert the multi-axial stress field into appropriate failure criteria:

1. Calculating yield criteria such as von Mises (distortion-energy) or Tresca (maximum shear stress), and using the maximum and minimum stress (= 0 in RCF) to calculate stress amplitude and mean stress (Refs. 6, 7).

2. Finding the maximum and minimum shear stress at every sub-surface point and calculating shear stress amplitude and mean stress (= 0 for f=0 due to symmetric shear stress).

Figure 2 shows the comparison of all three criteria as a function of sub-surface depth. All three criteria show a similar sub-surface distribution with a maximum stress between 0.15 and 0.3 mm. Differences occur especially at the surface, at which the shear stress is zero. Von Mises and Tresca stresses are compressive stresses (R = infinity); stress amplitude and mean stress would be half of the calculated data. The shear stress represents the amplitude with σmean = 0 (R = –1).

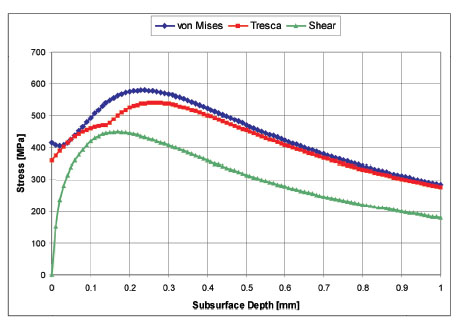
Figure 2—Comparison of Failure Criteria–1,800 MPa f=0.

The sub-surface stress distribution, the position and width of the area of maximum sub-surface stress, and therefore the volume of material exposed to the highest stress, are affected by the type of contact (point, elliptical, and line), the relative curvature of the bodies in contact, the Young’s moduli, and the contact pressure. This is different from most conventional fatigue tests, in which the point or volume of maximum stress is almost independent of the load level. This difference can play an important role for RCF strength under variable loading conditions.

Failure Modes Under RCF Loading
Figure 3 illustrates the three most important failure modes for RCF conditions (Refs. 13, 14):

1. Surface-induced cracks. There are two different cracking modes possible:

a) Surface cracks, which usually grow according to the shear component at 30° into the material.

b) Micropitting or gray-stained areas at which many very small surface cracks form. Micropitting most frequently occurs in surface-hardened steels in the regime of mixed lubrication. If lubrication is restored, micropitting may arrest; otherwise micropits may grow and damage the material.

2. Sub-surface cracks are usually formed in the region of the highest von Mises stress. They first grow parallel to the surface and turn toward the surface, forming the pitting.

3. Core crushing or sub-case fatigue (which should not be confused with sub-surface cracking) occurs deep within the material and is usually caused by insufficient heat treatment.

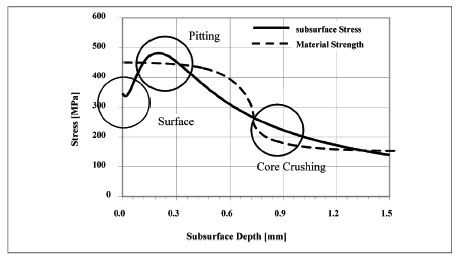
Figure 3—Failure modes in RCF.

In order to compare the effect of materials and/or process parameters on the RCF strength, it is absolutely essential to identify the failure mode, which in most cases requires intense failure analyses.

Aspects of Material RCF Strength
Analyzing the sub-surface stress field provides design limits for failure under operational loading conditions. If a correlation could be established to other well-known material and fatigue properties, a prediction of lifetime of mating parts in RCF would be possible, and the reliability of gears and transmissions, even under variable loading conditions, could be determined.

The compressive character of the stress state in RCF has been summarized as follows (Ref. 5):

1. The tendency to yield is quite small, hence a substantial pressure may be sustained before the onset of plasticity.

2. Deformation is very ductile, and even normally brittle materials show considerable ductility.

3. If, as is often the case, all three principal stresses are negative, the likelihood of brittle fracture is small, since the only possible growth regime of cracks is shear.

4. Crack growth by fatigue is a complicated process, controlled possibly by shear stress as well as tension and considerably influenced by the presence of residual stresses and surface treatments.

Despite its helpfulness to interpret failure modes under RCF, it must be emphasized that von Mises and Tresca criteria are yield criteria for materials under tension loading and do not correlate to yielding and fatigue under multi-axial compressive stresses. According to fracture mechanic principles, conventional fatigue data, and crack growth experiments, cracks will not grow under pure compressive stresses (Refs. 5, 8). Therefore, conventional material data, including fatigue data obtained under tension loading, cannot be used to predict the RCF strength of a material.

The fully reversed shear stress component is frequently assumed to be the parameter controlling the RCF strength, which would correspond to the fracture stress intensity factor in Mode II (Ref. 6). Experimentally supported data that would sustain a correlation between RCF strength and fully reversed shear fatigue tests do not exist. Furthermore, due to the fact that the shear stress at the surface is zero (without sliding – s = 0) or very small (fully EHD conditions f<0.1) it does not explain surface-induced failure modes.

In contradiction to fatigue under tension loading, RCF data show that there is no endurance limit and that failure occurs after very high numbers of load cycles (Refs. 9, 10). It is assumed that the slope of the S-N curve does not change, even at high numbers of load cycles. The effect is important in determining reliability under variable loading conditions and the contribution of small-load amplitudes to crack growth and damage in general.

In order to estimate the effect of material and process parameters on RCF strength, the sub-surface microhardness profile is most often used and compared to the sub-surface von Mises stress. The hardness of the material is somehow related to the strength (RCF strength) of the material. This method is successfully applied when case depth is optimized as a function of relative radius of flank curvature in gear design (Refs. 11, 12). For PM, it is a combination of case depth and porosity level at the surface and sub-surface regions. Gears with different equivalent curvatures show similar lifetimes when the case depth is adjusted according to the von Mises sub-surface stress.

Factors Affecting RCF Performance
External factors influence rolling contact fatigue strength by affecting contact conditions, sub-surface stress distribution and failure mode. RCF strength is also affected by material physical properties, micro-structural phases and micro-constituents. Despite many years of RCF and gear testing, the effect of individual factors on the RCF strength of materials is still not fully understood. Necessary tests to study the effect of each parameter individually and systematically are time-consuming and cost-intensive.

Surface Friction and Sliding. Surface shear stress due to relative sliding and friction affects the sub-surface stress distribution. The shear component τxy becomes asymmetrical with regard to the line of contact. The stress components σxx, σyy, σzz in the line of contact are no longer principal stresses. The amplitude of the shear stress is only affected in the near surface region, but the stress ratio shifts into more negative values (from R=–1 to R =–1.3 at 1,800 MPa, f = 0.1). The maximum von Mises stress (Fig. 4) increases, shifts out of the line of contact, and moves closer towards the surface. The surface stress is also increased and can exceed the magnitude of the sub-surface stress at higher coefficients of friction (f >0.3).

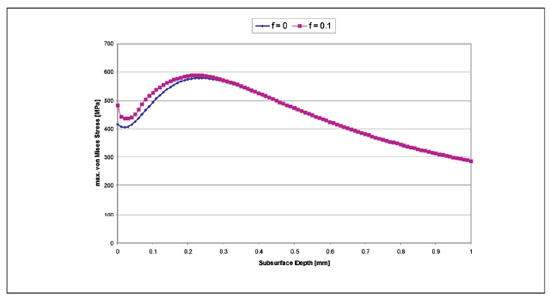
Figure 4—Comparison maximum von Mises stress, with and without friction.

Sliding in gears occurs at every point of the line of contact except at the pitch point. Sliding is positive in the addendum and negative in the dedendum of the tooth profile (Ref. 9). Experience shows that most pitting occurs in the dedendum of teeth at negative sliding (Refs. 13–15). There is only one comprehensive research program that determined the RCF strength of different materials at different sliding ratios (Ref. 16). Results confirm that the RCF strength is reduced by sliding and is leveling off at about –24% (Fig. 5). Due to the fact that the tests were carried out under full EHD lubrication and the coefficient of friction was below f = 0.1, the decrease in RCF strength cannot be explained by the change of the sub-surface stress distribution alone.

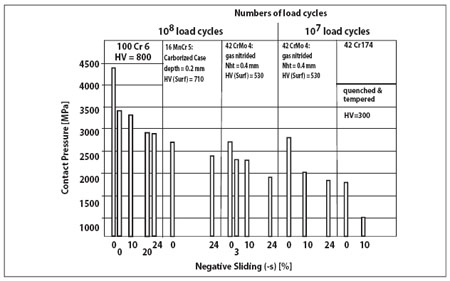
Figure 5—Effect of sliding of RCF strength of gear materials (Ref. 16).

Lubrication. The lubrication regime plays an important role in the RCF strength of the material. In mixed lubrication, the coefficient of friction increases significantly, increasing surface stress and surface wear. Therefore, full EHD lubrication is preferred when determining the RCF strength of the material. In full EHD lubrication, elastic relaxation of the contact bodies at the exit of the contact zone compresses the lubricant. This leads to a spike in the contact pressure that may exceed it by up to 30% (Refs. 13, 14).

Surface Topography. The surface topography affects the RCF strength by an inhomogeneous distribution of the contact pressure over the contact area. There is a higher pressure in high asperities that can lead to localized plastic deformation and crack initiation. Secondly, if lubricant is trapped in surface pockets during over-rolling, i.e., if the dimension of the pocket is small relative to the patch width, the lubricant is compressed by the elastic deformation of the surrounding material, producing a high hydrostatic pressure within the pocket (Fig. 6 a and b) (Ref. 17). Grain boundaries within the pocket are sites for crack initiation. PM materials may additionally be affected when the manufacturing process leaves surface porosity.

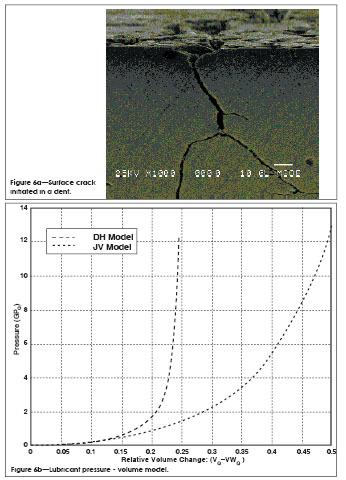
Figure 6—Effects of trapped lubricant in surface dents.

Inclusions and soft spots. Inclusions and soft spots within the microstructure can act as sites for crack nucleation. Increased purity of the materials shifts the failure mode more and more toward the surface, and the RCF strength is determined by surface conditions. Soft spots, such as retained austenite and Ni-rich phases in PM steels, may be detrimental to RCF strength. Under compressive forces, retained austenite may transform into martensite, therefore increasing compressive residual stresses and fatigue strength. However, if the grains of retained austenite are completely embedded in martensite, the volume increase caused by the transformation from austenite to martensite may lead to microscopic tension stresses which may support crack opening and growth. The effect of Ni-rich phases on RCF strength of surface-densified PM steel will be discussed later in this article.

Residual Stresses. It is common knowledge that compressive residual surface stresses can enhance the fatigue strength of materials (Refs. 18, 19). Most gears are therefore case-hardened, which produces the proper compressive sub-surface residual stresses. However, the sub-surface residual stress distribution changes due to rolling contact fatigue (Refs. 12, 20). There are still compressive residual stresses in the near surface region, but they are drastically reduced or even turned into tension stresses in the region of maximum sub-surface von Mises stress. These changes in residual stresses could explain the existence of tension stresses necessary for crack opening and crack growth.

Initial Conclusions
Two very important conclusions can be drawn from analysis of failure modes under RCF loading:

1. The RCF strength of a material cannot be predicted. If the microstructure-process-property correlation has not been established, extensive testing is the only way to determine the magnitude of the RCF strength and the factors that affect it.

2. Crack initiation is the most important failure criterion, and it is an essential part for determining and analyzing the failure mode. Most RCF test rigs use catastrophic pitting as failure criterion because pitting results in excess machine vibration and can signal stopping. However, the final pitting characterizes the end-point of the failure, not the initiation of failure. In order to identify the failure mode after the pitting occurs, intensive microstructural analyses are necessary to identify crack origin and crack propagation path.

Gear Designer Requirements
Transmission designers face a big challenge: On one hand, they are forced to reduce weight and increase load carrying capacity of gears and/or power densities of transmissions, and yet find new, cost-effective materials and manufacturing processes to be competitive in the global market. Several sets of data are required to perform reliability calculations and to minimize the risk of a premature failure (Refs. 18, 19):

1. The load-time history must be known, either by calculation or by direct measurement.

2. The S-N curve (50% probability of survival) must be known for the selected material and heat treatment, which is the basis for applying Miner’s rule to determine the cumulative damage sum (Refs. 21, 22).

3. The scattering of the fatigue data must be known to calculate the safety factor for a certain probability of failure.

Data are usually available for traditional materials and conventional heat treatments, based upon long years of experience and extensive tests. In order to realize cost savings offered by newly developed materials or processes, the designer requires not only the standard set of material data, but also the statistical variation of the process over a long period of time. Furthermore, relying on more than a single vendor requires comparable technologies and process control methods used by all suppliers in order to exclude additional data scattering due to process variations.

Most companies use statistical methods to keep the manufacturing process in control. However, in order to identify property-relevant process parameters, systematic studies of the effect of those parameters on critical material properties are essential. If those data are not available, extensive tests on prototypes under real-life loading conditions are necessary and required.

There is no doubt that the request for systematic investigations of material/process effects is in the best interest of both partners—the manufacturer and the end-user. The burden shifts to the test engineer to develop test procedures that would provide both partners with the necessary data in a reasonable time frame and acceptable costs. Those model tests pay off over time because they lead to confidence in the capability of new materials and technologies, and provide the database for quality assurance and further improvements.

The RCF Test Bench
The RCF test rig used in this program was developed by ZF Friedrichshafen, Germany, in the early 1960s in order to study RCF at test conditions that simulate live gear contacts. The rig was used in extensive research programs in Germany in connection with the Gear Research Institute of the Technical University in Munich (Refs. 16, 23–25) and was used for the first study of RCF strength of PM steels (Ref. 26). A detailed description of the test rig has been published (Refs. 13, 26, 27).

Figure 7 shows the basic principle of the RCF test rig. The test sample is located in the center of the machine and loaded by three load rolls. The contact force is applied by hydraulic pressure of the lubricant, which furthermore provides the required amount of oil to produce full EHD lubrication in the contact zone. By changing the gear ratio of the gear drive, the relative velocity of the load rolls in regard to the test specimen (the sliding ratio) can be easily varied within a wide range.

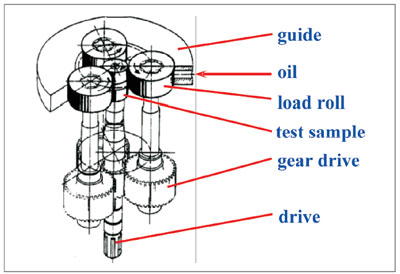
Figure 7—Principle of the RCF test bench.

The test rig offers features that make the unit especially feasible for model testing of materials for gear applications:

1. The design allows cylindrical test surfaces, resulting in line contact, which is normal in gears. If required, crowned test samples can be used, resulting in elliptical contact. The cylindrical surface allows testing of original, native surfaces that are manufactured using the same gear manufacturing process. Due to the fact that the surface topography becomes more and more important, including the actual surface topography is an essential part of model testing. The surface becomes even more important for manufacturing processes, such as PM processes, that produce a unique surface structure.

2. Establishing full EHD lubrication is essential for determining the real material RCF strength, and doing so excludes additional effects such as uncontrollable surface friction and wear.

3. Full EHD lubrication is also a necessary condition to use crack detection technologies. The test rig used in this program is equipped with an eddy current sensor (Fig. 8), which allows the detection of cracks in the very early stage of nucleation (Refs. 3, 15). Therefore, the failure criterion used is the initiation of first cracks.

Figure 8—Eddy current technology used with the RCF test bench [Refs. 3,15].

4. Eddy current technology allows the monitoring of crack growth. However, there is no direct correlation between the actual size of the flaw and the magnitude of the eddy current signal. Therefore, calculation of crack propagation rate uses a modified Paris’ equation in which the actual eddy current signal indicates flaw size (Refs. 3, 15).

5. The eddy current technology can be used to determine the threshold for crack growth. By pre-cracking test specimens, stepwise reducing the load, and monitoring the eddy current signal, the contact pressure can be determined at which the crack stops growing (Ref. 3). If such a threshold exists, it could be assumed that it represents the true endurance limit of the material, and that contact pressures below that level do not contribute to the damage sum and can be dismissed in reliability calculations and/or tests under variable loading conditions.

6. The machine is equipped with a variable drive, which allows testing samples at different surface velocities. The standard speed is between 3,000 and 3,600 rpm, which results in 540,000 to 648,000 load cycles per hour.

7. The load is controlled by hydraulic pressure. Changing the level of contact pressure can be done automatically using a servo-hydraulic control valve. This allows tests under variable loading conditions to simulate real operational conditions.

8. As is common with every RCF test rig, the ZF-RCF test bench is equipped with a vibration sensor that shuts off the machine when pitting leads to excessive vibration of the machine. Therefore, tests up to the occurrence of the final, catastrophic failure can be performed.

Table 1 summarizes the standard test conditions used for the test programs included in this paper.

Test Results for Wrought Steels
AISI 5120 and AISI 8620 Carburized. Both wrought steels are very common materials used in today’s automotive transmissions, and performance of both materials under operational conditions is well known. Therefore, both materials can serve as benchmark material in RCF investigations. Other materials and/or processes can also be benchmarked.

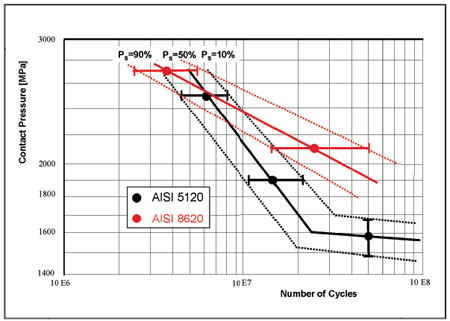
Figure 9—S-N curves of benchmark materials (AISI 5120 and 8620).

Figure 9 contains the S-N curves of both materials for final pitting. In the time life region, five test samples per load level were used. A staircase test with 15 specimens has been performed at AISI 5120 and 50 million load cycles. To determine test data scattering, data were plotted in a log-normal diagram and the number of load cycles for probability of survival of 90% and 10% determined graphically. The scattering can be expressed in terms of the probability of survival by

Equation (1): TN = 1: T10% / T90%

with:

TN = Factor for the scattering of the number of load cycles.

T10% = Number of load cycles for 10% probability of survival.

T90% = Number of load cycles for 90% probability of survival.

Using the eddy current technology, the number of load cycles for the occurrence of first cracks has been determined for both the materials at a contact pressure of 2,100 MPa. The results are given in Table 2.

The analyses of the first cracks (Fig. 10) reveal that, in both cases, the failure is surface initiated. The cracks show the typical crack growth at 30° from the surface and branching toward the surface. The cracks propagate until they reach the region of maximum sub-surface stress and turn horizontally, forming the pitting by branching toward the surface. The failure mode indicates that the surface topography plays an important role and that the true RCF strength of both materials may be higher.

Figure 10—SEM pictures of first cracks.

The crack propagation rate (Fig. 11a & b) is very comparable to crack propagation in tension. The Paris’ exponent, which represents the slope of the log (da/dN) vs. log (ΔK) plot, is within the range of wrought materials under tension. That might be an indicator that even at the compressive stress field, tension stresses may be responsible for crack growth. More research is necessary, however, to generalize those findings.

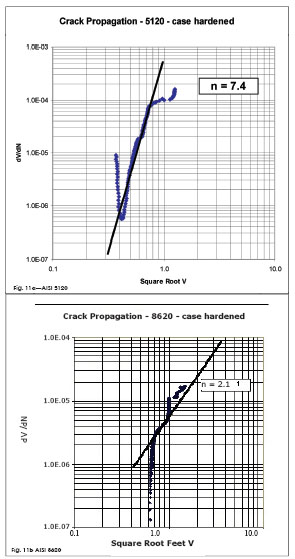
Figure 11—Crack propagation rate.

AISI 1060 and AISI 4150—Induction Hardened. Induction hardening is a second heat treatment to produce favorable surface conditions for RCF applications. Due to the higher carbon content of the material, the core hardness might be higher compared to carburized steel, and the case depth is deeper as well. Both materials were tested at a contact pressure of 2,100 MPa. The number of load cycles for the first crack and the final pitting are shown in Table 3.

As can be seen from Figure 12, AISI 1060 fails by initiating sub-surface cracks at the region of the highest sub-surface stress, while AISI 4150 shows a surface-induced crack that turns horizontally at the region of maximum sub-surface stress. The surface profile (Figure 13) indicates that the surface roughness may play an important role in the failure mode. Figure 14 shows that the crack propagation rate (expressed by the Paris’ exponent) of the investigated materials is also within the range of those typically experienced under tension loading.

Figure 12—SEM pictures of first cracks.

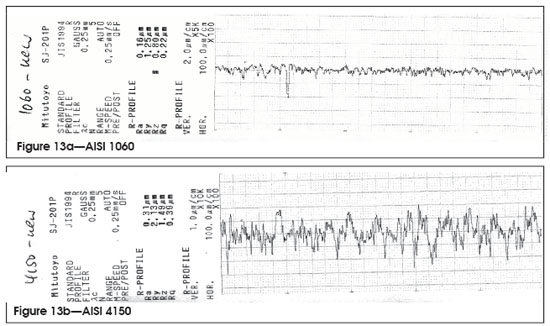
Figure 13—Surface Profile Before Test.

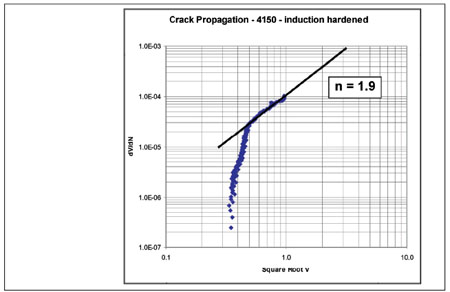
Fig. 14a—Crack propagation rate. AISI 4150 at 2,100 MPa.

AISI 1060 was tested for the threshold for crack growth. Pre-cracked specimens (at 1,900 MPa) were tested at lower load levels, the crack propagation was monitored and the number of load cycles before final failure was recorded. Table 4 summarizes the results. Figure 14b shows the crack propagation rates at different load levels.

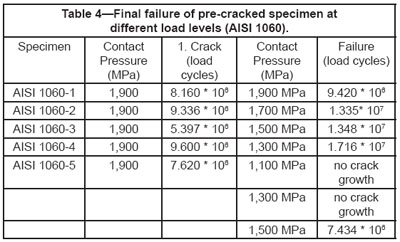
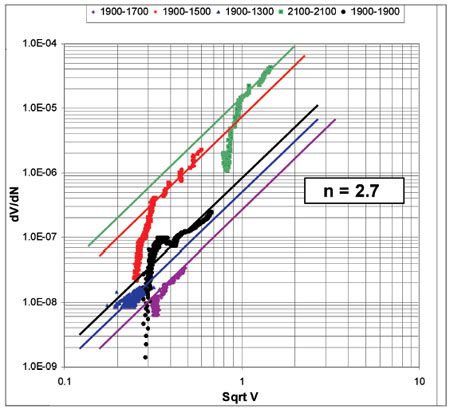
Figure 14b—Crack Propagation Rate. AISI 1060—different load levels.

There are some very important conclusions that can be drawn from the test results:

1.There is a threshold for crack growth. There was no crack growth for more than 10 million load cycles at 1,100 MPa. This threshold level is surprisingly high.

2. After running the test at 1,100 MPa, the load level was increased stepwise until renewed crack growth could be seen. The load increased by two steps before crack growth occurred. It seems as if load levels at or below the threshold lead to compressive residual stress at the crack tip, which would explain the incubation time for renewed growth.

3.The crack propagation rate at all investigated load levels is very similar and independent of the load itself. This may be another indication that the crack growth is actually governed by tension stresses at the crack tip.

Discussion
The combination of full EHD lubrication and eddy current technology opens a completely new opportunity to study and optimize materials and/or processes for RCF applications. The detection of first cracks allows the analysis of failure modes. Monitoring the eddy current signal over time gives information about the crack propagation and threshold for crack growth. This offers—for the first time—the chance to study the effects of material and process parameters systematically. It is believed that improvement as well as decline of the RCF strength due to variation of those parameters can be determined with only a few test samples, which would drastically accelerate test programs. The savings in test time is especially evident in the determination of the threshold for crack growth. With eddy current monitoring, this can be done in days, instead of weeks with conventional test procedures, which use load levels required for 100 million or more load cycles until failure.

References

1. Hoffmann, G., J.A. Rice, “Initiation and Propagation of Cracks in Wrought and Sintered Steels During Rolling Contact Fatigue,” Advances in PM & Particulate Materials, MPIF, 2005, reprinted in APMI PM Industry News Online, Vol. 3, No. 3, March 2006.

2. “Development of Tools to Determine the Effect of PM Manufacturing Parameters on RCF of Highly Loaded Gears,” NSF– SBIR Phase I Grant No. 0510141, 2005.

3. Hoffmann, G., F.G. Hanejko, R.H. Slattery, “Crack Initiation and Propagation in RCF—A New Approach to Understanding Pitting Failure in Highly Loaded Gears,” SAE Technical Papers, SAE 2006-01-0383, 2006, published in SP-2039, ISBN 0-7680-1774-2, SAE 2006.

4. Hoffmann, G., F.G. Hanejko, R.H. Slattery, “Effect of Process Parameters on Crack Initiation and Propagation in Rolling Contact Fatigue,” Advances in PM & Particulate Materials, MPIF, Princeton, 2006.

5. Hills, D.A., D. Nowell, A. Sackfield, “Mechanics of Elastic Contacts,” Butterworth-Heinemann Ltd., Oxford 1993.

6. Contact Problems—Software provided by D.A. Hills, University of Oxford, United Kingdom.

7. Dieter, G.E. Mechanical Metallurgy, McGraw-Hill, Third Edition, 1986.

8. K.-H. Schwalbe, “Bruchmechanik metallischer Werkstoffe,” Carl Hanser Verlag Muenchen-Wien, 1980.

9. Dudley, D.W., “Handbook of Practical Gear Design,” CRC Press, ISBN 1566762189, 1994.

10. “Design Guide for Vehicle Spur and Helical Gears,” American National Standard–ANSI/AGMA 6002-B93, AGMA.

11. “Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth,” American National Standard - ANSI/AGMA 2001-D04, AGMA.

12. Tobie, T., P. Oster, B.R. Hoehn, “Systematic Investigation of the Influence of Case Depth on the Pitting and Bending Strength of Case Carburized Gears,” Gear Technology, Vol. 22, No. 4, pages 40–48, 2005.

13. Hoffmann, G., K. Lipp, “Design for Rolling Contact Fatigue,” 2002 Advances in Powder Metallurgy & Particulate Materials, Conference Proceedings 2002 P/M World Congress, Orlando, FL, MPIF 2002.

14. Hoffmann, G., K. Lipp, “Design for Rolling Contact Fatigue,” International Journal of Powder Metal, p. 33–46, Vol. 39, No. 1,2003.

15. “Appearance of Gear Teeth–Terminology of Wear and Failure,” American National Standard - ANSI/AGMA 1010-E95, AGMA.

16. Roesch, H. “Untersuchungen zur Waelzfestigkeit von Rollen – Einfluss von Werkstoff, Waermebehandlung und Schlupf, ”1976, Dissertation (Ph.D. Thesis), Technische Universitaet Muenchen, Muenchen, Germany.

17. Zhao, J., F. Sadeghi, H.M. Nixon, “A Finite Element Analysis of Surface Pocket Effects in Hertzian Line Contact,”, Journal of Tribology, p. 47-54, Vol. 122, No.1, January 2000.

18. Stephens, R.I., A. Fatemi, R.R. Stephens, and H.O. Fuchs, “Metal Fatigue in Engineering,” John Wiley & Sons, Inc., Second Edition, 2001.

19. Sonsino, C.M., “Fatigue Design Concepts,” ISBN: 1-878954-91-1, MPIF Princeton, 2003.

20. G. Kotthoff, “ Neue Verfahren zur Tragfaehigkeitssteigerung von gesinterten Zahnraedern,” Dissertation (Ph.D. Thesis), RWTH Aachen, Germany, 2003.

21. Palmgreen, A.“Die Lebensdauer von Kugellagern,” VDI-Z, Vol. 68, No. 4, 1924.

22. Miner, M.A., “Cumulative Damage in Fatigue,” Journal Applied Mechanics, Vol. 12, No. 3, 1945.

23. Winter, H., H. Roesch, “Einfluss des Schlupfes auf die Waelzfestigkeit von Rollen,” Antriebstechnik, Vol. 14, No. 9, 1975.

24. Kaeser, W., “Beitrag zur Gruebchenbildung an gehaerteten Zahnraedern,” Dissertation (Ph.D. Thesis), Technische Universitaet Muenchen, Muenchen, Germany, 2003.

25. Hornung, K., “Zahnraeder aus Bainitischem Gusseisen mit Kugelgraphit,” Dissertation (Ph.D. Thesis), Technische Universitaet Muenchen, Muenchen, Germany, 1983.

26. Lipp, K., “Oberflaechenzerruettung von Sinterstaehlen unter konstanter und veraenderlicher Hertzscher Pressung mit ueberlagerter Reibung (Schlupf),” Dissertation (Ph.D. Thesis), Universitaet des Saarlandes, Saarbruecken, Germany, 1997.

27. Hoffmann, G., K. Lipp, K. Michaelis, C.M. Sonsino, J.A. Rice, “Testing P/M Materials for High Loading Gear Applications,” International Journal of Powder Metallurgy, Vol. 34, No. 6, 1999.

William Jandeska is a consultant with Midwest Metallurgical Ltd. in the field of automotive material, applications and processes. He retired after 34 years at General Motors—20 at the GM Research Lab and 14 as a staff engineer in the advanced materials and processing group at GM Powertrain. Jandeska is a fellow of the ASM Metallurgical Society and APMI—The Powder Metallurgical Institute.

Gottfried Hoffmann is president of V-Tech International, a testing service provider and consulting company in general fatigue design and durability studies, located in Milwaukee. In addition, he teaches part-time at several universities in Milwaukee and is a member of MPIF and APMI. Hoffmann was the winner of the 2002 PM World Conference’s Outstanding Technical Paper Award.