Prediction of Surface Zone Changes in Generating Gear Grinding
Prediction of Surface Zone Changes in Generating Gear Grinding
One process for hard finishing gears is generating gear grinding. Due to its high process efficiency, generating gear grinding has replaced other grinding processes such as profile grinding in batch production of small- and middle-sized gears. Yet despite the wide industrial application of generating gear grinding, the process design is based on experience along with time- and cost-intensive trials. The science-based analysis of generating gear grinding demands a high amount of time and effort, and only a few published scientific analyses exist. In this report a thermo-mechanical process model that describes influences on the surface zone in generating gear grinding is introduced.
Introduction and Motivation
In order to improve load carrying capacity and noise behavior case hardened gears usually are hard finished (Ref. 1). One possible process for hard finishing of gears is generating gear grinding. Generating gear grinding has replaced other grinding processes in batch production of small and middle sized gears due to the high process efficiency.
Despite the wide industrial application of this process, only a few scientific analysis exist (Refs. 2–5), because the science-based analysis of generating gear grinding needs a high amount of time and effort and the continuously changing contact conditions complicate the investigation.
The lack of knowledge of causeeffect relationships results in an empirical process design in industrial practice. Therefore in most cases several trials must be performed to find a stable process design. By stock fluctuation or by an unfavorable process design an undesirable process result up to a process-related thermal damage of the external zone can occur. Therefore it is necessary to get a better understanding of the cause-effect relationships between process parameters, tool specifications and process in generating gear grinding.
State of the Art
Hard finishing technology is used to remove deviations from hardening, to machine tooth flank modifications and to meet quality requirements. The case hardening process is necessary to enable the gear to transmit high torque with smaller gears in high power applications. In industrial applications generating gear grinding, profile gear grinding and gear honing are most commonly used as hard finishing processes for gears. Each of these high-performance processes is using geometrically undefined cutting edges. Continuous generating gear grinding has evolved to the dominant process in batch production for small and middle sized gears due to the high productivity.
Generating gear grinding. One of the most efficient processes for hard finishing of gears in batch production of external gears and gear shafts is generating gear grinding. Generating gear grinding is used for hard finishing of gears with a module of mn = 0.5 mm to mn = 10 mm (Refs. 6, 4). By the application of new machine tools the process can be used for grinding large module gears with an outside diameter up to da = 1,000 mm (Ref. 7).
The cylindrical grinding worm, whose profile equates a rack profile in a transverse section, meshes with an external gear (Fig. 1, left). The involute is generated by continuous rolling motion of grinding worm and workpiece by the profile cuts method (Refs. 8, 4). Profile cuts method in generating processes means that the profile form is generated by a finite number of profiling cuts. Due to the closed grinding worm no generating cut deviations, as in gear hobbing process, occur during generating gear grinding.
In generating gear grinding multiple points of the grinding worm are in contact simultaneously. The number of contact points changes continuously during tool rotation (Fig. 1, right).
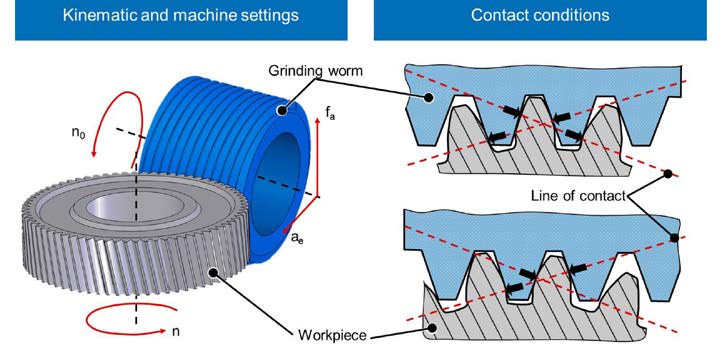 Figure 1 Generating gear grinding: principle, machine settings, and contact conditions (Ref. 9).
Figure 1 Generating gear grinding: principle, machine settings, and contact conditions (Ref. 9).In comparison to other gear grinding processes the stock removal rate in generating gear grinding is very high. In most cases the stock removal rate is limited by the demanded gear quality (Ref. 4). Furthermore, the appearance of a detrimental process-related surface zone inducement (grinding burn) can be the limiting factor.
Publications (Refs. 10–12), and the doctoral thesis of Meijboom (Ref. 2), Türich (Ref. 3) and Stimpel (Ref. 5) show the influence of several parameters on the process results. But several technological correlations have not been analyzed or verified in experimental trials yet.
Current challenges. Due to limited scientific studies the technology users, grinding tool suppliers and machine tool manufactures face two main challenges.
On the one hand the process design and optimization is based on knowhow of the process user. In cases, where no sufficient experience (e.g., new gear geometry, new grinding tools) exists, cost-intensive trials have to be performed to find a favored and robust process design. In this case, several trial iterations are usually necessary to obtain high process stability. In order to reduce the number of needed iteration loops the technological cause-effect relationships must be analyzed in detail.
On the other hand, the demand for increasing productivity leads to an increase of axial feed and cutting speed. With an increase of productivity the cutting force and thus the heat flow towards the workpiece are rising. This in turn leads to an increased risk of grinding burn during the grinding process. The challenge is to increase the productivity without causing grinding burn.
Research Objective and Approach
The research objective for generating gear grinding at WZL is the increase of process efficiency and process reliability in generating gear grinding by description of the technological cause-effect relationships for cutting forces as well as for occurrence of grinding burn in a model. For the analysis of the cause-effect relationships an analogy trail has been developed and will be introduced in this report.
The aim of this report is to present a model to predict grinding burn for generating gear grinding. Therefore cutting forces in analogy trails are measured and the interactions between process parameters and occurred grinding burn are taken into account. The measured cutting forces will be combined in an empirical cutting force model. With the ability to calculate the cutting force the heat flow density towards the workpiece can be estimated. With a comparison of the heat flow density and the grinding burn occurrence a critical heat flow density that leads to grinding burn can be determined. Thereby a model to predict grinding burn can be derived. In conclusion the prediction model will be transferred onto generating gear grinding and will be validated by generating gear grinding trials.
Analogy trail for Generating Gear Grinding
The complexity of the contact conditions between tool and workpiece during generating gear grinding complicates the analysis of generating gear grinding. On the one hand, the penetration volumes change over the tooth profile height during grinding. On the other hand, the number of engaged tool flanks and workpiece flanks is variable. To investigate generating gear grinding on a single fixed point on the tooth profile, a geometrickinematic model, the analogy trail, has been developed (Refs. 12, 9). The principle of the analogy trail for generating gear grinding is shown (Fig. 2).
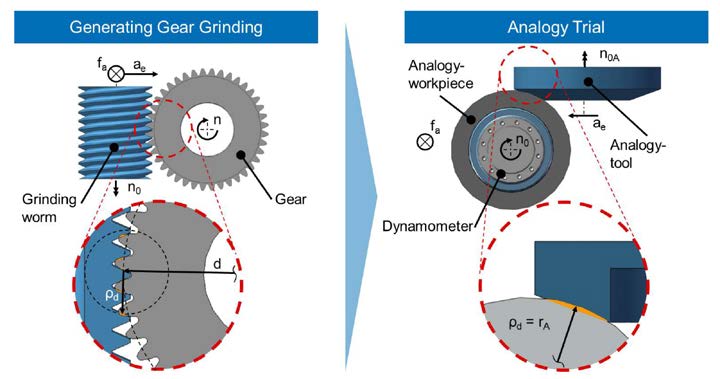 Figure 2 Analogy trial for generating gear grinding: principle and deduction of analogy
workpiece geometry (Ref. 9).
Figure 2 Analogy trial for generating gear grinding: principle and deduction of analogy
workpiece geometry (Ref. 9).For each point of the involute the local radius of curvature ρy can be calculated (Ref. 13). For the analogy trail the contact conditions at different positions of the involute can be approximated. The radius of the workpiece in the analogy trail rA equals the radius of curvature at the investigated point of the involute profile. Thus the diameter of the analogy workpiece depends on the number of teeth z, the module mn, the helix angle β and the pressure angle αn of the mapped sample gear. The rack profile of the grinding worm can be approximated in the investigated contact point by a face wheel with a conic working surface (Ref. 9).
Besides the workpiece and the tool geometry the chip geometry in the analogy trail has to be comparable to the chip geometry in generating gear grinding.
Therefore the cutting length lcuA and the chip thickness hcuA have to be comparable between analogy trail and generating gear grinding.
Furthermore the kinematics of chip formation and the velocities must be fitted to generating gear grinding. During chip formation the lateral sliding speed vtA, the axial feed speed vaA and the cutting speed vc interfere with each other. The cutting speeds in generating gear grinding and analogy trail are the same. The lateral sliding speed vtA can be calculated by the rotational speed nA of the workpiece and the requirement to be synchronous. The axial feed speed vaA can be adjusted according to the generating gear grinding process as the product of rotational speed nA and axial feed fa. Rotational speed as well as axial feed in analogy trail and generating gear grinding is identical. The tool is a grinding wheel with an angled surface. The angle corresponds to the pressure angle αn0 of the grinding worm.
The mapped grinding process and the machine tool used are shown (Fig. 3).
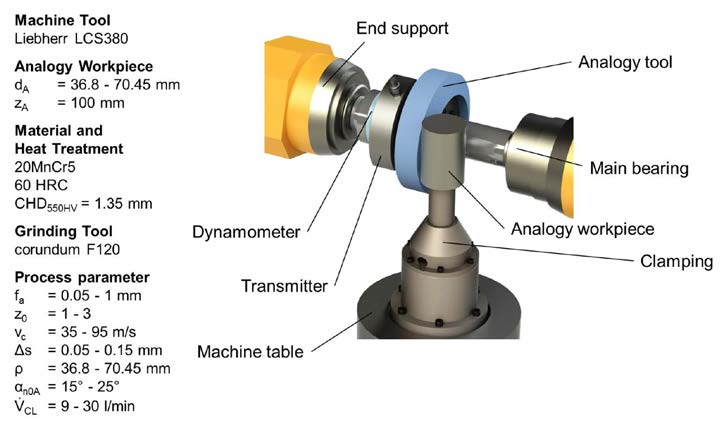 Figure 3 Workpiece data and machine tool.
Figure 3 Workpiece data and machine tool.The experimental set-up of the analogy trails is shown (Fig. 4);
 Figure 4 Experimental set-up analogy trial generating gear grinding.
Figure 4 Experimental set-up analogy trial generating gear grinding.With this experimental set-up, 129 analogy trails were performed. In these analogy trails the following process parameters were taken into account. The axial feed fa, the number of starts z0, the cutting speed vc, the stock Δs, the pressure angle of the analogy tool αn0A and the cooling lubricant volume flow VCL. In addition, the diameter of the analogy workpiece was varied to investigate different points on the involute profile.
Prediction Model for Surface Zone Inducements
Based on the empirical data of the analogy trails an empirical-physical model is built up in the following. Using the model, the occurrence of a process-related damage of the surface zone can be predicted. For this purpose, an approach to describe the surface zone inducement is presented. Subsequently the required parameters are determined and the prediction model is derived.
Analytical model approach. To predict the surface zone inducement the heat flow density, which describes the energy flow in the contact zone between tool and workpiece, must be determined. To prevent grinding burn the heat flow density towards the workpiece qw must always be lower than a critical heat flow density qw, crit that leads to a detrimental influence on the surface zone.
The heat flow density towards the workpiece qw corresponds to the current energy flow through the contact area between tool and workpiece Ac. In general for grinding the majority of the cutting energy is thermal energy, which is produced by intense friction, shear and separation processes as well as by friction of the abrasive grain and bond (Ref.14). Assuming that also for generating gear grinding almost all cutting power is converted into thermal energy, the total energy flow in the contact area can be calculated by the product of cutting force Fc and cutting speed vc. In order to estimate the heat flow density towards the workpiece qw correction factors must take the distribution of the heat flow from the contact zone into account. These corrections factors are KCLF which takes into account the cooling lubricant flow and KW which considers the heat flow towards the workpiece. With these factors the heat flow density towards the workpiece qw can be estimated with Equation 1(Ref. 15) as:
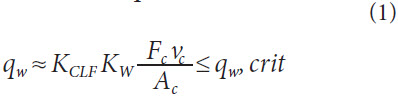
Determination of model parameters. In the following, the correction factors KCLF and KW, the cutting force Fc and the contact area between workpiece and tool Ac must be determined to calculate the heat flow density. With correlation of the known heat flow density and the occurrence of grinding burn for every trial the critical heat flow density can be determined
Cutting Force
The cutting force was measured during the analogy trails with a dynamometer. During the analogy trails various process parameters were investigated to get a statement about the influence on the cutting force. In order that the cutting force does not have to be determined empirically for each combination of process parameters, a cutting force model is derived in the following.
The cutting force model is set up based on the obtained data from the analogy trails using a regression analysis. For regression analysis, the influence of the process parameters axial feed fa, number of starts z0, cutting speed vc, stock Δs, cooling lubricant flow VCL and tool pressure angle αn0A are considered. The regression analysis of the cutting force is carried out with a cubic approach considering the interactions. For regression analysis, the significance level was set to α = 0.05. The comparison of the calculated forces using the force model and the measured forces is shown (Fig. 5).
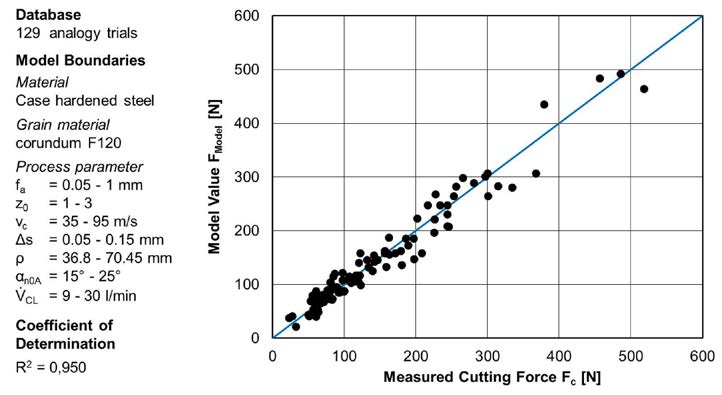 Figure 5 Model results and observations of the cutting force.
Figure 5 Model results and observations of the cutting force.In summary it can be stated that the cutting force model maps the measured cutting forces very well and offers a high stability due to a widely varying database. Thus, the cutting force model is suitable as a basis for calculating the heat flow density and to derive a prediction model for surface zone changes for generating gear grinding.
Contact Area
To define the heat flow density the contact area between tool and workpiece must be calculated. The contact area Ac between tool and workpiece is corresponding to the zone of heat transfer between tool and workpiece. The contact area for the analogy trails can be calculated with a penetration calculation considering various stocks and axial feeds. Figure 6 shows the contact area for a constant pairing of tool and workpiece over axial feed. For an axial feed of fa < 0.2 mm, the contact area drops sharply. For an axial feed of fa < 0.08 mm no penetration volume between workpiece and tool could be calculated with the penetration calculation.
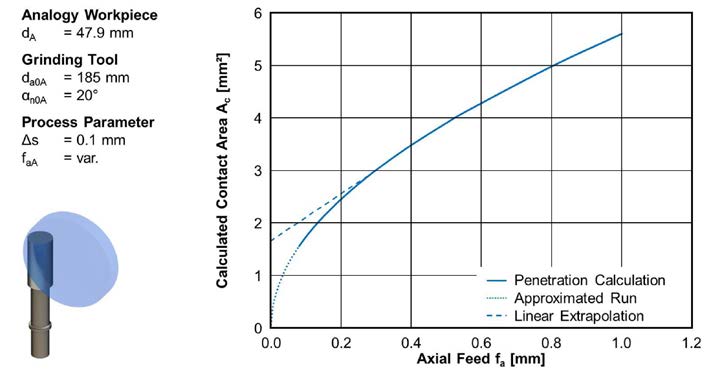 Figure 6 Determination of contact area.
Figure 6 Determination of contact area.Due to numerical inaccuracies, the calculated contact area for small axial feeds is not exact. From kinematics it can be derived that in the absence of axial feeding a contact between tool and workpiece must exist for the first rotation of tool and workpiece. The contact area for low axial feeds of fa < 0.25 mm is calculated from an axial feed by linear extrapolation. The extrapolated contact area is indicated by the dotted line in the diagram. Using this functional relationship, the contact area Ac can be determined for the prediction model.
Correction Factors
Finally, the two correction factors to calculate the heat flow density must be determined. The heat distribution for each combination of tool, workpiece and cooling lubricant is different and variable over the contact zone (Ref. 16). Due to the different thermal material parameters such as specific heat capacity cp and thermal conductivity λ, as well as the inability to determine the temperatures in the con-
tact zone, the heat distribution factor KW cannot be calculated for generating gear grinding. In several studies heat distribution factors have been estimated for different grinding processes (Refs.17–22). The evaluation of these papers shows that up to 80% of the thermal energy can flow into the workpiece. For surface grinding of unhardened steel a heat distribution factor KW = 0.65 was determined (Ref. 19). A heat distribution factor for grinding of hardened 20MnCr5 cannot be found in the literature. Because of the poor accessibility of the contact area during generating grinding a heat distribution factor KW = 0.8 is assumed in this work. This corresponds to the standard assumptions in literature and provides an assessment on the safe side (Refs. 23–24).
In addition to the constant heat distribution factor KW, a variable factor KCLF to determine the influence of the cooling lubricant flow is necessary. For this purpose, the heat flow densities of the analogy trails were normalized to the maximum heat flow density and analyzed in relation to the cooling lubricant flow. Using a regression analysis the influence of the cooling lubricant flow on the heat flow density was determined.
The normalized heat flow density qnorm at constant process parameters decreases with increasing cooling lubricant flow (Fig. 7).
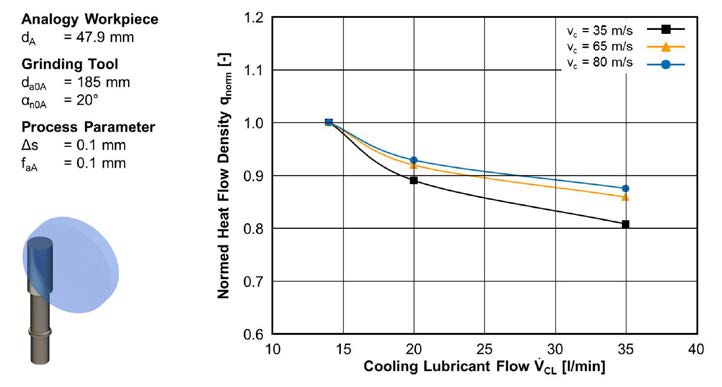 Figure 7 Determination of correction factor for consideration of cooling lubricant.
Figure 7 Determination of correction factor for consideration of cooling lubricant.For constant cutting speeds, the heat flow towards the cooling lubricant can be approximated by an exponential function depending on the cooling lubricant flow VCL. The correction factor KCLF can be described by Equation 2. The factors a and b were determined as a function of cutting speed using regression analysis. The coefficient of determination for the equation of the correction factor KCLF is:
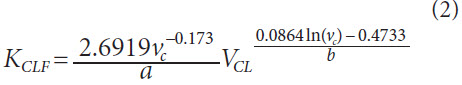
The energy flow towards the workpiece can be estimated by the product of the two correction factors KW, KCLF and the cutting power. Depending on the cutting speed and cooling lubricant flow, the percentage of the energy flow towards the workpiece is between 60% and 80% of the total cutting power.
Empiric analytical prediction model. Based on the empirical knowledge of cutting force and the analytical considerations of an analytical heat flow density an empirical-analytical prediction model is derived in the following. The model is used to predict the process-related influences on the surface zone taking into account the heat flow density towards the workpiece.
Using the presented empirical force model and the mathematical description of the model parameters, the heat flow density can be calculated for every trial. In addition to the magnitude, the residence time of the heat flow density also has a major impact on the influence on the surface zone. The residence time of the heat flow density for one point on the surface equals the contact time tc between tool and workpiece for the same point. The contact time for generating gear grinding can be calculated with Equation 3, (Ref. 25).
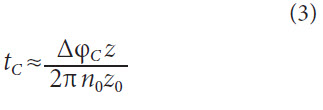
As with tool and process variables, the contact time is also dependent on the workpiece geometry. The contact time is calculated by the rotational speed of the tool n0, the number of starts z0, the number of teeth of the workpiece z and the rolling angle of the cutting width Δφc. The rolling angle describes the required arc segment, which must be passed in order to achieve the width of contact between tool and workpiece at the respective profile point.
For the analogy trails, the heat flow density is plotted against the contact time (Fig. 8).
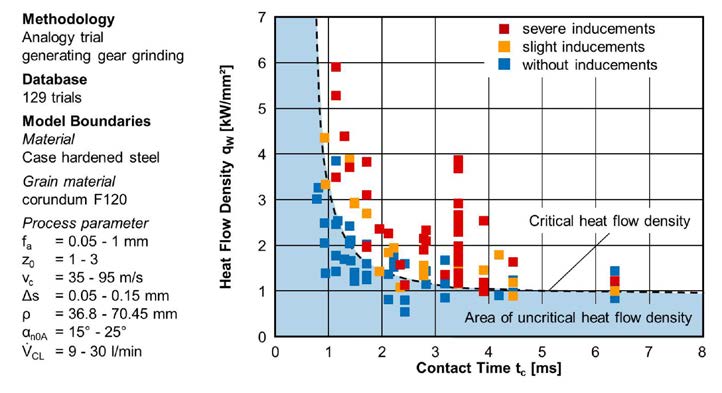 Figure 8 Surface zone inducements depending on heat flow density.
Figure 8 Surface zone inducements depending on heat flow density.The analysis shows that for a short contact time a high heat flow density can flow into the workpiece without causing damage. In contrast, at long contact times only a low heat flow density is necessary to harm the surface zone. With increasing contact time, the critical limit asymptotically approaches a constant level. From this distribution, the contact time depending limit of the critical heat flow density can be determined from the graph and described mathematically.
The calculated critical heat flow density is shown as a black dashed line in the graph. Considering the simplified assumptions for the calculation of the correction factors as well as the contact time and the dispersion of results, a very well approximation for determining the critical heat flow density can be found.
In summary it can be stated that the empirical-analytical model is suitable to determine the critical limit, which leads to grinding burn. However, it must be determined whether the model, which is based on analogy trail results, can be applied to actual generating gear grinding. For this purpose, the prediction model must first be validated with the sample gear that is mapped in the analogy trail.
Validation of the Prediction Model
The prediction model constructed on basis of analogy trails is compared and validated in the following with results from generating gear grinding trials. First, the transferability of the model to generating gear grinding is validated. For this purpose grinding tests are carried out with the sample gear that is mapped in the analogy trail. Subsequently, the model is validated on an additional gear.
Transfer to generating gear grinding. For the validation of the prediction model a deductive approach is chosen in the following. The general model was applied to a particular case to validate the findings. For the gear that is mapped in the analogy trail, the heat flow densities have been calculated for each set of process parameters. The classification of heat flow densities and surface zone inducements in the analytical empirical prediction model is shown in Figure 9.
 Figure 9 Model validation for sample gear.
Figure 9 Model validation for sample gear.The results of generating gear grinding trials were arranged in the characteristic field of the heat flow density of the prediction model. The heat flow densities shown are calculated for the pitch circle diameter of the sample gear. The degree of influence on the surface zone has been marked in analogy to the previous illustrations. The range of non-critical heat flow density is identical due to the geometric relationship between analogy trail and sample gear.
All points for which no detrimental surface zone inducement was observed after generating gear grinding are with one exception within the non-critical area. The heat flow densities of the components with slight and severe detrimental inducements are larger than the calculated critical heat flow density of the prediction model.
The evaluation shows that the prediction model is able to predict the occurrence of grinding burn in good accuracy for the sample gear. The results of the generating gear grinding trials reflect the determined findings and identified relationships from the analogy trail. Thus, the prediction model has been validated for the sample gear. Whether the prediction model can be applied to additional gears must be examined in the following.
Validation with additional gears. In order to test the transferability of the empirical-analytical prediction model, the model is applied to another spur gear. Therefore further generating gear grinding trials were performed.
The design of experiments was defined by using the prediction model. For this, the process parameters were predicted for both clearly damaged and not affected tooth flanks. The gears have been inspected after grinding by means of nital etching to evaluate and document surface zone inducements.
As a second application a planetary gear of a construction machine is selected. In contrast to the previous gear, the present gear has a higher module and a higher face width. The gear geometry and further details of material and heat treatment can be found in Figure 10.
 Figure 10 Gear geometry of planetary gear.
Figure 10 Gear geometry of planetary gear.The results of the second gear geometry are shown (Fig. 11);
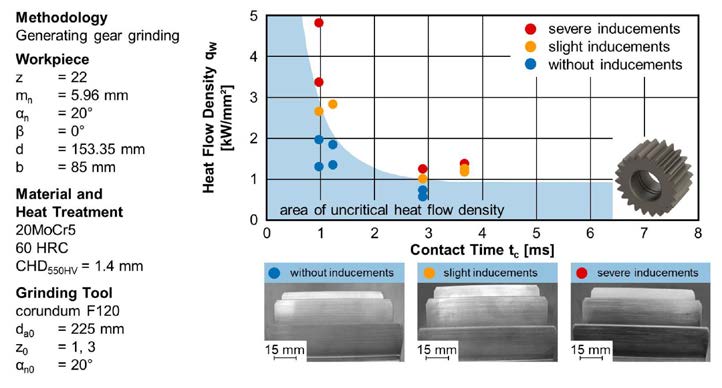 Figure 11 Application of prediction model for planetary gear.
Figure 11 Application of prediction model for planetary gear.The calculated critical heat flow density for the pitch circle diameter limits the damaged and non-damaged gears with a good accuracy. Different forms of surface zone inducements are shown in the lower part of Figure 11. All workpieces with a detrimental inducement show a damaged zone near the tip area.
Severely damaged components show a dark coloration over a large part of the profile. In addition to the qualitative statement about whether surface zone damage is to be expected, the heat flow density can be calculated on the basis of the local approach for any point of the gear flank.
To explain the process-related detrimental inducement in the tooth tip area, the distribution of the heat flow density has been calculated for a process design for the entire tooth profile. The results are compared with results of nital etching in Figure 12.
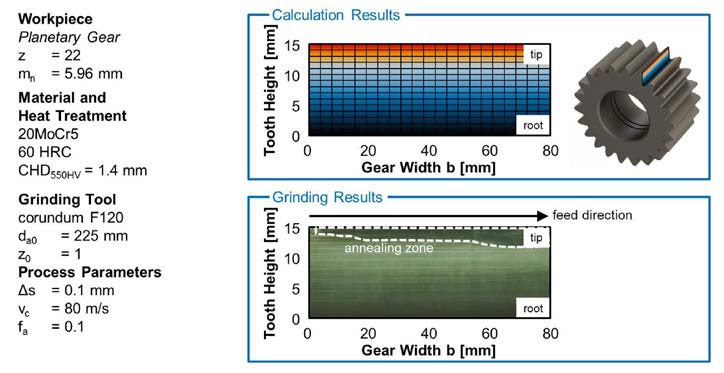 Figure 12 Comparison of local heat flow density and process results.
Figure 12 Comparison of local heat flow density and process results.The occurrence probability of a surface zone inducement is marked in color on the tooth height. In the black and blue areas no surface zone inducement is to be expected. In the transition between the light blue and the yellow area there may be a slight damage. In the tooth tip area, the critical heat flow density is exceeded and therefore a damaged surface zone is expected. This area is marked in red.
The distribution over the tooth height can be explained by the cause-effect relationships, determined in the analogy trails. With an increase in the radius of curvature the cutting forces increase as well. This results in a varying heat input over the tooth profile. The highest cutting force and therefore the largest heat flow density on the tooth flank is present at the tooth tip. This result is well-correlated with the results of nital etching.
In feed direction the affected zone is growing in contrast to calculation results. The main reason for the expansion of the damaged zone is wear of the grinding worm. With increasing machining time also the friction and therefore the cutting force as well as the heat flow density increases. In the prediction model the wear of the grinding wheel is not taken into account. For this reason, predicted and actual damage differ.
By applying the predictive model to an additional gear, the applicability was tested for other geometries. It turns out that the prediction model derived from the analogy trail can also be used to predict a detrimental inducement of the surface for additional geometries.
Summary and Outlook
The thermo-mechanical surface zone inducement is an important quality criterion for functionality of gears. Also for generating gear grinding it is necessary to determine thermal and mechanical loads and their influencing factors to avoid damage of the surface zone.
The research objective of this report was to derive a model to describe and predict detrimental surface zone inducements for generating gear grinding. Therefore, the necessary model parameters and correction factors were determined. Subsequently, the model was validated using two gear geometries.
The objective of this report was met through validation of the predictive model. The model for predicting detrimental surface zone inducements will help increase the efficiency and process reliability of continuous generating gear grinding and improve the description and understanding of the technological cause and effect relations.
In the next step the derived empirical analytical prediction model should be linked with a manufacturing simulation. The combination of a local determination of chip geometries and the automated calculation of the existing model parameters will allow widespread use of the model in industrial applications. Furthermore, it will significantly improve the process design and optimization in continuous generating gear grinding. In addition, the cutting force model can be extended with a link to a manufacturing simulation. With the help of calculated chip geometries it is likely possible to find a correlation between chip geometries and the measured cutting forces.
Besides the optimization of the model a further development of the analogy trail is possible. With the analogy trail, an evaluation of the performance of grinding worms for generating gear grinding can be performed. So on the one hand, a pre-selection of grinding worm specifications is possible and on the other hand the wear behavior could be analyzed better due to the simple geometry of the grinding tool.
 Dipl.-Ing. Matthias
Ophey studied mechanical
engineering at RWTH Aachen
University with a focus on
production engineering.
Upon graduation in 2013 he
became a scientific research
assistant in the gear
department of the Laboratory of Machine Tools
and Production Engineering (WZL). Ophey’s
research is dedicated to focusing on hard
finishing of gears — especially generating gear
grinding, and manufacturing-related properties.
Dipl.-Ing. Matthias
Ophey studied mechanical
engineering at RWTH Aachen
University with a focus on
production engineering.
Upon graduation in 2013 he
became a scientific research
assistant in the gear
department of the Laboratory of Machine Tools
and Production Engineering (WZL). Ophey’s
research is dedicated to focusing on hard
finishing of gears — especially generating gear
grinding, and manufacturing-related properties. Dr. Jan Reimann is a 2008
graduate of RWTH Aachen
University, having studied
mechanical engineering
with a focus on production
engineering. He began
working in 2008 — first
as scientific research
assistant and later as
team leader — in the gear department of the
Laboratory of Machine Tools and Production
Engineering (WZL). While there he has
published his doctoral thesis on generating
gear grinding. Today Reimann is a production
engineer at Siemens Mechanical Drives in
Bocholt, focusing on manufacturing technology
development.
Dr. Jan Reimann is a 2008
graduate of RWTH Aachen
University, having studied
mechanical engineering
with a focus on production
engineering. He began
working in 2008 — first
as scientific research
assistant and later as
team leader — in the gear department of the
Laboratory of Machine Tools and Production
Engineering (WZL). While there he has
published his doctoral thesis on generating
gear grinding. Today Reimann is a production
engineer at Siemens Mechanical Drives in
Bocholt, focusing on manufacturing technology
development.References:
- Schlattmeier, H. Diskontinuierliches Zahnflankenprofilschleifen mit Korund, Dissertation, RWTH Aachen, 2003.
- Meijboom, L. Erhöhung der Wirtschaftlichkeit beim Wälzschleifen durch Verbesserung des Zerspannvorgangs, Dissertation, RWTH Aachen, 1979. 3. Türich, A. Werkzeugprofilerzeugung für das Verzahnungsschleife, Dissertation, Universität Hannover, 2002.
- Bausch, T., Moderne Zahnradfertigung. Verfahren und Maschinen zur kostengünstigen Herstellung von Stirn- und Kegelrädern mit hoher Qualität, 3. Auflage, Expert Verlag, Renningen- Malmsheim, 2006.
- Stimpel, F.Technologische Kenngrößen für das kontinuierliche Wälzschleifen von Evolventenverzahnungen, Dissertation, Universität Hannover, 2009.
- Klocke, F. and König, W., Fertigungsverfahren Band 2: Schleifen, Honen, Läppen. 4. Auflage, VDIVerlag, Düsseldorf, 2005.
- Reichel, F. Verfahrensauswahl beim Schleifen von Großverzahnungen, Seminar: Feinbearbeitung von Zahnrädern, WZL der RWTH Aachen, November 2007.
- Sulzer, G. Werkzeugmaschinen zum Feinbearbeiten der Zahnradflanken von vorverzahnten Zahnrädern, Europäische Patentschrift EP0282046, Liebherr Verzahntechnik, Kempten, 1993
- Klocke, F., C. Gorgels, and J. Reimann. Generating Gear Grinding – New Possibilities in Process Design and Analysis, AGMA Fall Technical Meeting 2011, 11FTM02, ISBN 978-1- 61481-001-8.
- Klocke, F., C. Gorgels and J. Reimann. Analyse des kontinuierlichen Wälzschleifens mithilfe der Durchdringungsrechnung, In: 50. Arbeitstagung „Zahnrad und Getriebetechnik“, Hrsg.: Klocke, F.; Brecher, C., Eigendruck Getriebekreis Aachen, S.14-1 - 14-40, 2009.
- Klocke, F., C. Gorgels and J. Reimann. Kontinuierliches Wälzschleifen von Verzahnungen – Softwareunterstützte Prozessoptimierung, In: WB Werkstatt und Betrieb, Jg. 142, Heft 5, S.62- 63, 2009.
- Klocke, F., C. Gorgels and J. Reimann. Ansatz für ein Prozesskraftmodell für das kontinuierliche Wälzschleifen von Verzahnungen, In: 51. Arbeitstagung „Zahnrad und Getriebetechnik“, Hrsg.: Klocke, F.; Brecher, C., Eigendruck Getriebekreis Aachen, S.8-1 - 8-40, 2010.
- DIN 3960. Begriffe und Bestimmungsgrößen für Stirnräder (Zylinderräder) und Stirnradpaare (Zylinderradpaare) mit Evolventenverzahnung, Hrsg. Deutscher Normenausschuss, März 1987.
- Vits, R. Technologische Aspekte der Kühlschmierung beim Schleifen, Dissertation, RWTH Aachen, 1985.
- Takazawa K. Effects of Grinding Variables on Surface Structure of Hardened Steel, In: Bulletin of the Japan Society of Grinding Engineers, Volume 2, S. 14-21, 1966.
- Hoffmeister, H.-W and B. Denkena. Jahrbuch Schleifen, Honen, Läppen, Polieren: Verfahren und Maschinen, Vulkan-Verlag, Essen, 63. Ausgabe, ISBN 3-802-72941-2, Oktober 2007.
- Gorgels, C. Entstehung und Vermeidung von Schleifbrand beim diskontinuierlichen Zahnflankenprofilschleifen, Dissertation, RWTH Aachen, 2011.
- Grof, H.E. Beitrag zur Klärung des Trennvorgangs beim Schleifen von Metallen, Dissertation, TU München, 1977, 15 14FTM02. 19. Hoffmeister, H.-W. and H.K. Tönshoff. Jahrbuch Schleifen, Honen, Läppen, Polieren: Verfahren und Maschinen, Vulkan-Verlag, Essen, 61. Ausgabe, 2004.
- Lowin, R. Schleiftemperaturen und ihre Auswirkungen im Werkstück, Dissertation, RWTH Aachen, 1980.
- Rowe, W.B., S.C.E. Black, B. Mills, H.S. Qi and M.N. Morgan. Experimental Investigation of Heat Transfer in Grinding, In: Annals of the CIRP, Volume 44/1/1995, S. 329-332.
- Steffens, K. Thermomechanik des Schleifens, Dissertation, RWTH Aachen, 1983.
- Heinzel, C. Schleifprozesse verstehen: Zum Stand der Modellbildung und Simulation sowie unterstützender experimenteller Methoden, Habilitation, Universität Bremen, 2008.
- Tönshoff, H.K., J. Peters, I. Inasaki and T. Paul. Modelling and Simulation of Grinding Processes, In: CIRP Annals 41(2):677–688, 1992.
- Schriefer, H., W. Thyssen, W., Wirz, G. Scacchi and M. Gretler. Kontinuierliches Wälzschleifen von Verzahnungen, 1. Auflage, Eigenverlag Reishauer AG, Wallisellen, 2008.






